
【题目】如图,四边形ABCD为菱形,AB=BD,点B、C、D、G四个点在同一个圆⊙O上,连接BG 并延长交AD于点F,连接DG并延长交AB于点E,BD与CG交于点H,连接FH,下列结 论:①AE=DF;②FH∥AB;③△DGH∽△BGE;④当CG为⊙O的直径时,DF=AF.其中正确结论的个数是( )
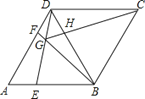
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】∵四边形ABCD为菱形,AB=BD,∴△ABD是等边三角形,∵B,C,D,G四个点在同一个⊙O上,∴∠GDC+∠GBC=180°,又∠BDC=∠DBC=60°,∴∠GDB+∠GBD=60°,又∠ADE+∠EDB=60°,∴∠ADE=∠DBF.在△ADE和△DBF中,∠A=∠ADB,AD=DB,∠ADE=∠DBF,∴△ADE≌△DBF,∴AE=DF,故①正确;∵B,C,D,G四个点在同一个⊙O上,∴∠DCG=∠DBG,又∠DBG=∠ADE,
∴∠ADE=∠DCG.在△ADE和△CDH中,∠A=∠BDC,AD=DC,∠ADE=∠DCG,∴△ADE≌△DCH,∴AE=DH,又DF=AE,∴DF=DH.又∠ADB=60°,∴∠DFH=60°,∴FH∥AB,故②正确;由△ADE≌△DCH,得∠AED=∠DHC,∴∠DHG=∠DEB,又∠ADE=∠DBG,∴∠EDB=∠FBE,∴△DGH∽△BGE,故③正确;当CG为⊙O的直径时,∠GBD=30°,又∠ADB=60°,∠DFB=90°,∵△ADB是等边三角形,∴DF=AF,故④正确.故选D.


科目:初中数学 来源: 题型:
【题目】利民种子培育基地用A、B、C三种型号的玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广.通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图(图1、图2):
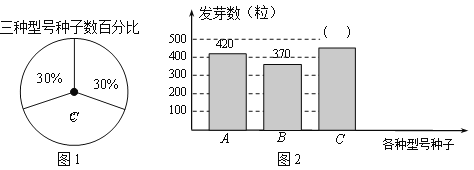
(1)C型号种子的发芽数是_________粒;
(2)直接写出应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放到一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.

(1)已知A(![]() 2,3),B(5,0),C(
2,3),B(5,0),C(![]() ,
, ![]() 2).
2).
①当![]() 时,点A,B,C的最优覆盖矩形的面积为 ;
时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,则t的值为 ;
(2)已知点D(1,1),点E(![]() ,
, ![]() ),其中点E是函数
),其中点E是函数![]() 的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
的图像上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到该商品售价13%的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.求:
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】集合M={x|1<x+1≤3},N={x|x2﹣2x﹣3>0},则(RM)∩(RN)等于( )
A.(﹣1,3)
B.(﹣1,0)∪(2,3)
C.(﹣1,0]∪[2,3)
D.[﹣1,0]∪(2,3]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com