
【题目】如图,在直角坐标系中放入一个边长OC=8,CB=10的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE
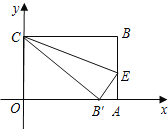
(1)求B′点的坐标;
(2)求折痕CE所在直线的解析式.
【答案】(1)点B′的坐标为(6,0);(2)直线CE的解析式为y=﹣![]() .
.
【解析】
试题分析:(1)由翻折的性质可知B′C=BC=10,然后由勾股定理可求得OB′的长,从而得到点B′的坐标;
(2)由OB′=6可知B′A=4,由翻折的性质可知BE=B′E,然后再Rt△EB′A中由勾股定理可求得AE=3,从而得到点E的坐标,最后利用待定系数法求得直线CE的解析式即可.
解:(1)由翻折的性质可知B′C=BC=10.
在Rt△OCB′中,由勾股定理得:OB′=![]() =
=![]() =6.
=6.
∴点B′的坐标为(6,0).
(2)∵OA=10,OB′=6,
∴B′A=4.
由翻折的性质可知B′E=BE.
设B′E=BE=x,则AE=8﹣x.
在Rt△B′AE中,由勾股定理AE2+B′A2=B′E2,即(8﹣x)2+42=x2
解得:x=5cm.
∴AE=8﹣5=3.
∴点E的坐标为(10,3).
设CE的解析式为y=kx+b.
将点C和点E的坐标代入得:![]() .
.
解得:k=﹣![]() ,b=8.
,b=8.
∴直线CE的解析式为y=﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则ABCD的周长为( )
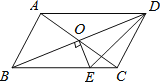
A.8cm B.12cm C.16cm D.24cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016重庆市第6题)下列调查中,最适合采用全面调查(普查)方式的是 ( )
A.对重庆市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对重庆新闻频道“天天630”栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省舟山市第5题)某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的( )
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如[2.7] =2,[-4.5] =-5;计算[3.7] + [-6.5] 的值为( )
A.-2 B.-3C.-4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】期中考试后,班里有两位同学议论他们所在小组同学的数学成绩,甲说:“我们组成绩是88分的同学最多”,乙说:“我们组的11位同学成绩排在最中间的恰好也是88分”,上面两位同学的话能反映处的统计量分别是( )
A. 众数和平均数 B. 平均数和中位数 C. 众数和方差 D. 众数和中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com