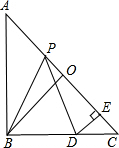
(1)证明:∵O是等腰直角三角形ABC斜边AC的中点,
∴OB⊥AC;∠OBC=

∠ABC=45°,
又∵DE⊥AC,∴∠BOP=∠PED=90°,
∵AB=BC,∠ABC=90°,
∴∠C=∠A=45°,
∵∠PDB=∠C+∠DPE,
∴∠PDB=45°+∠DPE,
∵PB=PD,
∴∠PBD=∠PDB,
∴∠PBO+45°=45°+∠DPE
∴∠PBO=∠DPE,
∵在△POB和△DEP中,

,
∴△POB≌△DEP(AAS),
∴PE=BO;
故PE与BO的位置关系是PE⊥BO,大小关系是:PE=BO.
(2)解:∵O是等腰直角三角形ABC斜边AC的中点
∴OB=

AC,OB⊥AC,
∵AC=2,∴PE=OB=1,∵AP=x,∴CE=2-1-x=1-x,
∴S
△APB=

x•1=

x
∵DE⊥AC,∠C=45°,DE=CE=1-x,
∴S
△DEC=

(1-x)
2∴S
四边形PBDE=S
△ABC-S
△APB-S
△DEC
∴y=

×2×1-

x-

(1-x)
2∴y=-

x
2+

x+

.
分析:(1)利用等腰直角三角形的性质得出OB⊥AC,即可得出PE与BO的位置关系,再利用全等三角形的判定得出△POB≌△DEP(AAS),得出PE与BO的大小关系;
(2)利用S
四边形PBDE=S
△ABC-S
△APB-S
△DEC,分别求出各图形面积,得出y与x之间的函数关系即可.
点评:此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,根据已知图形正确分割出三角形是解题关键.

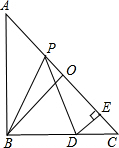 如图,在等腰直角Rt△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.
如图,在等腰直角Rt△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.  (1)证明:∵O是等腰直角三角形ABC斜边AC的中点,
(1)证明:∵O是等腰直角三角形ABC斜边AC的中点, ∠ABC=45°,
∠ABC=45°, ,
, AC,OB⊥AC,
AC,OB⊥AC, x•1=
x•1= x
x  (1-x)2
(1-x)2 ×2×1-
×2×1- x-
x- (1-x)2
(1-x)2 x2+
x2+ x+
x+ .
.

 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
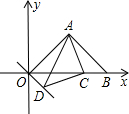
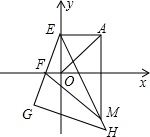

 如图:在平面直角坐标系中,△ABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数y1=
如图:在平面直角坐标系中,△ABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数y1=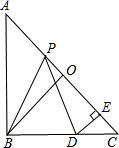 如图,在等腰直角Rt△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.
如图,在等腰直角Rt△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.