
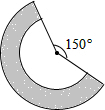
 如图所示,大扇形半径为R,小扇形半径为7厘米.
如图所示,大扇形半径为R,小扇形半径为7厘米.科目:初中数学 来源: 题型:
 如图所示,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.
如图所示,有一直径是1m的圆形铁皮,要从中剪出一个最大的圆心角是90°的扇形ABC.查看答案和解析>>
科目:初中数学 来源:中考加速卷 数学 题型:044
电工想用一块长AB=5cm,宽BC=4cm的矩形钢板ABCD做出一个面积尽可能大的扇形,他设计了两种方案.(以下数据解题时供参考:![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .)
.)

(1)如图①直接从钢板上割下扇形ABP,请你求出此时圆心角α1的大小.
(2)如图②先在钢板上沿对角线切割下两个扇形,再焊成一个如图③所示的大扇形ABC(不计接缝),请你求出此时的扇形ABC的圆心角α2,并与α1比较大小.
(3)根据方案(1)、(2)的思路和计算结论,请你在图④中再设计一种切割、焊接的方案,使得扇形钢板的半径与(1)、(2)中的扇形半径相同,从而圆心角更大,因而面积也更大(不计接缝).
查看答案和解析>>
科目:初中数学 来源:2006年初中数学总复习下册 题型:044
现有总长为8 m的建筑材料,如图,用这些建筑材料围成一个如图所示的扇形花坛.当这个扇形的半径为多少时,可以使这个花坛的面积最大?并求最大面积.
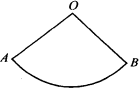
查看答案和解析>>
科目:初中数学 来源:2012年浙教版初中数学九年级上3.6圆锥的侧面积和全面积练习卷(解析版) 题型:解答题
小明要在半径为1m,圆心角为60°的扇形铁皮上剪取一块面积尽可能大的正方形铁皮.小明在扇形铁皮上设计了如图所示的甲、乙两种方案剪取所得的正方形的面积,并计算哪个正方形的面积较大?(估算时 取1.73,结果保留两个有效数字)
取1.73,结果保留两个有效数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com