

分析 (1)由阅读材料,可知路线1:l12=AC2=AB2+BC2=高2+底面周长一半2;路线2:l22=(高线AB+底面直径BC)2;将数据代入即可求出l12、l22的值,再运用差比法即可得出l1<l2;
(2)先根据阅读材料用含h、r的代数式分别表示l12、l22,再由l12>l22列出关于h、r的不等式,解不等式即可求解;
(3)先根据阅读材料将h=5代入,用含r的代数式分别表示l12、l22,再由l12=l22列出关于r的方程,解方程即可.
解答 解:(1)如图(2).
∵圆柱的底面半径为1厘米,高AB为5厘米,
∴路线1:l12=AC2=AB2+BC2=25+π2;
路线2:l2=AB+BC=5+2=7,l22=(AB+BC)2=49.
∵l12-l22=25+π2-49=π2-24<0,
∴l12<l22,
∴l1<l2,
∴选择路线1较短; (2)如图(2).
(2)如图(2).
∵圆柱的底面半径为r厘米,高为h厘米,
∴路线1:l12=AC2=AB2+BC2=h2+(πr)2=h2+π2r2,
路线2:l22=(AB+BC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h];
∵r恒大于0,
∴当(π2-4)r-4h>0,即$\frac{r}{h}$>$\frac{4}{{π}^{2}-4}$时,l12>l22,即此时选择的路2最短;
(3)如图(3),圆柱的高为5厘米.
l12=AC2=AB2+BC2=25+(2πr)2,
l22=(AB+BC)2=(5+4r)2,
由题意,得25+(2πr)2=(5+4r)2,
解得r=$\frac{10}{{π}^{2}-4}$.
即当圆柱的底面半径r为$\frac{10}{{π}^{2}-4}$厘米时,蚂蚁从点A出发沿圆柱表面爬行到C点的两条线段相等.
点评 本题考查了平面展开-最短路径问题,比较两个式子的大小,通常利用差比法,这里让这两个式子的平方相减.同时考查了学生的阅读理解能力,知识的迁移能力及分析问题解决问题的能力.


科目:初中数学 来源: 题型:选择题
| A. | 21时 | B. | 22时 | C. | 23时 | D. | 24时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
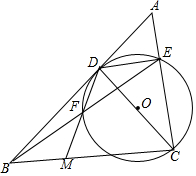 如图,在△ABC中,∠ACB=90°,点D在AB上,以CD为直径的⊙O交AC于点E,连接BE交⊙O于点F,延长DF交BC于点M,且∠BDF=∠DEB.
如图,在△ABC中,∠ACB=90°,点D在AB上,以CD为直径的⊙O交AC于点E,连接BE交⊙O于点F,延长DF交BC于点M,且∠BDF=∠DEB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
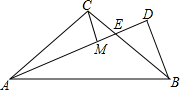 如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.
如图,Rt△ABC中,AC=BC,∠ACB=90°,若AE为∠BAC的角平分线,BD⊥AE,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com