
 如图,点D是等边△ABC边BC上一点,连接AD,作∠ADE=60°,交AC边于点E.若AB=3,BD=1,求CE的长.
如图,点D是等边△ABC边BC上一点,连接AD,作∠ADE=60°,交AC边于点E.若AB=3,BD=1,求CE的长. 分析 根据等边△ABC,可得∠B=∠C=60°,再根据有两组角对应相等的两个三角形相似,判定△ABD∽△DCE,得到$\frac{AB}{DC}$=$\frac{BD}{CE}$,进而求出CE.
解答 解:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠ADE=60°,
∴∠BAD+∠ADB=120°=∠CDE+∠ADB,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴$\frac{AB}{DC}$=$\frac{BD}{CE}$,即$\frac{3}{2}$=$\frac{1}{CE}$,
∴CE=$\frac{2}{3}$.
点评 本题主要考查了等边三角形的性质、相似三角形的判定及其性质的应用,解决问题的关键是判定相似三角形,依据相似三角形的对应边成比例列式计算.


科目:初中数学 来源: 题型:选择题
 某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )| A. | a=20 | |
| B. | b=4 | |
| C. | 若工人甲一天获得薪金180元,则他共生产50件 | |
| D. | 若工人乙一天生产m(件),则他获得薪金4m元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
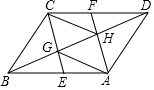 如图,在?ABCD中,点E,F分别是AB,CD边上的两点,且BE=DF,连接CE,AF,分别交BD于点G,H,连接AG,CH.
如图,在?ABCD中,点E,F分别是AB,CD边上的两点,且BE=DF,连接CE,AF,分别交BD于点G,H,连接AG,CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.
如图,在梯形ABCD中,AD∥BC,AE=DE,AC与BD相交于点E,∠ADB=60°,且BE:ED=3:1,BD=12,求梯形ABCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.
如图,四边形ABDC中,∠B=∠D=90°,BC=AB,以AB为直径的⊙O交BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com