
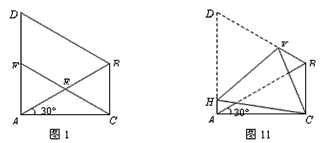
(1)① 在△ABC中,∠ACB=90°,∠CAB=30°,
∴ ∠ABC=60°.
在等边△ABD中,∠BAD=60°,
∴ ∠BAD=∠ABC=60° .
∵ E为AB的中点,
∴ AE=BE.
又∵ ∠AEF=∠BEC ,
∴ △AEF≌△BEC ;
② 在△ABC中,∠ACB=90°,E为AB的中点
∴ CE=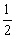 AB BE=
AB BE= AB,
AB,
∴ ∠BCE=∠EBC=60° .
又∵ △AEF≌△BEC,
∴ ∠AFE=∠BCE=60° .
又∵ ∠D=60°,
∴ ∠AFE=∠D=60° .
∴ FC∥BD
又∵ ∠BAD=∠ABC=60°,
∴ AD∥BC,即FD∥BC
∴ 四边形BCFD是平行四边形;
(2)∵∠BAD=60°,∠CAB=30°
∴∠CAH=90°
在Rt△ABC中,∠CAB=30°,设BC =a
∴ AB=2BC=2a,
∴ AD=AB=2a. 设AH = x ,则 HC=HD=AD-AH=2a-x.
在Rt△ABC中,AC2=(2a) 2-a2=3a2.
在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a-x) 2.
解得 x= a,即AH=
a,即AH=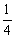 a.
a. 



 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
| PE |
| CE |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 明理由.
明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| BC2+CD2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=| DE |
| BD |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com