

分析 (1)先判断出△BCE≌△ACD,进而求出AD,再利用直角三角形斜边的中线等于斜边的一半即可;
(2)先判断出∠MAC=∠BCE,进而得出△MAC≌△ECB(SAS),即可得出结论;
(3)先求出∠PMC=30°,再根据勾股定理求出OB2=8+4$\sqrt{3}$,OC2=2,即可.
解答 (1)∵△ABC和△DEC都是等腰直角三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=90°,
∴△BCE≌△ACD(SAS),
∴AD=BE=2$\sqrt{5}$,
∵F为线段AD的中点,
∴CF=$\frac{1}{2}$AD=$\sqrt{5}$,
(2)如图,延长CF到M,使FM=FC,连接AM,DM,
又AF=DF,
∴四边形AMDC为平行四边形,
∴AM=CD=CE,∠MAC=180°-∠ACD,
∠BCE=∠BCA+∠DCE-∠ACD=180°-∠ACD,
即∠MAC=∠BCE,
又∵AC=BC,
∴△MAC≌△ECB(SAS),
∴CM=BE;∠ACM=∠CBE,
∴BE=CM=2CF;
∴∠CBE+∠BCM=∠ACM+∠BCM=90°,
即BE⊥CF;
(3)设BE、CF交于点P,过O作PM⊥BC;在BC上取一点N,使BN=PN.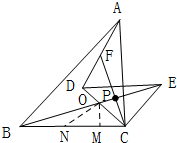
∵BE⊥CF,∠DCF=30°,
∴∠POC=60°,
∴∠PBC=∠POC-∠BCO=15°;
∴∠PMC=30°,
设PM=1,则OC=$\sqrt{2}$,ON=2,NM=$\sqrt{3}$,BN=2,
∴OB2=12+${({2+\sqrt{3}})^2}$=8+4$\sqrt{3}$,OC2=2,
∴$\frac{{O{B^2}}}{{O{C^2}}}$=4+2$\sqrt{3}$.
点评 此题是几何变换综合题,主要考查了直角三角形的性质,全等三角形的判定和性质,勾股定理,解本题的关键是∠MAC=∠BCE.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
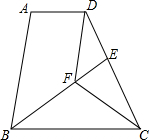 已知:如图,在四边形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:
已知:如图,在四边形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 9 | a | b | c | -5 | 1 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
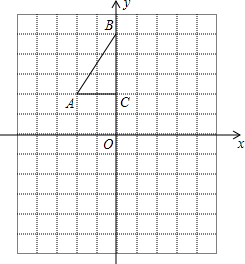 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com