如图，一次函数
的图象与反比例函数
的图象交于点
，与
轴交于点
.
（1）求一次函数的解析式和点的坐标；
（2）点C在x轴上，连接AC交反比例函数的图象于点P，且点P恰为线段AC的中点.请直接写出点P和点C的坐标.
（1）
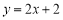；（-1,0）；（2）点P的坐标为（2，2）；点C的坐标为（3，0）.
【解析】
试题分析：（1）求出A点的坐标代入一次函数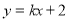
即可求出一次函数的解析式；令
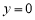，即可求得点
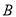的坐标.
（2）由点P恰为线段AC的中点和点P在反比例函数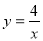
的图象上，求出点P的坐标，从而求出点C的坐标.
试题解析：（1）A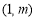
在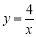
的图象上，∴
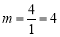．∴A点的坐标为
.
∵A点在一次函数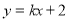的图象上，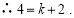
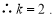
∴一次函数的解析式为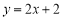
.
令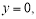
即
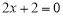，解得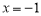
．
∴点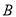的坐标为（-1,0）．
（2）∵A点的坐标为，点P恰为线段AC的中点，∴点P的纵坐标为2.
∵点P在反比例函数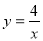的图象上，∴点P的坐标为（2，2）.
∵点P恰为线段AC的中点，∴点C的坐标为（3，0）.
考点：反比例函数和一次函数交点问题.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源：2015届云南省八年级上学期期末考试数学试卷（解析版） 题型：填空题
规定用符号[m]表示一个实数m的整数部分. 例如：[
]=0 ，[3.14]=3 ，按此规定[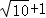
]的值为 _________ .
查看答案和解析>>
科目：初中数学 来源：2014年北京市西城区中考二模数学试卷（解析版） 题型：解答题
阅读下面材料:
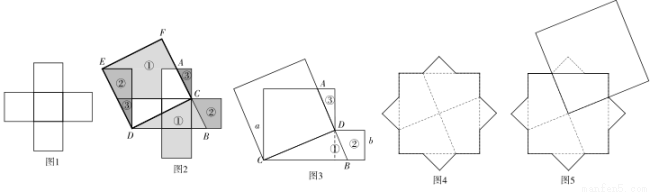
小明遇到这样一个问题: 如图1，五个正方形的边长都为1，将这五个正方形分割为四部分，再拼接为一个大正方形．
小明研究发现：如图2，拼接的大正方形的边长为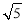
， “日”字形的对角线长都为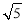，五个正方形被两条互相垂直的线段AB，CD分割为四部分，将这四部分图形分别标号，以CD为一边画大正方形，把这四部分图形分别移入正方形内，就解决问题．
请你参考小明的画法，完成下列问题：
（1）如图3，边长分别为a，b的两个正方形被两条互相垂直的线段AB，CD分割为四部分图形，现将这四部分图形拼接成一个大正方形，请画出拼接示意图
（2）如图4，一个八角形纸板有个个角都是直角，所有的边都相等，将这个纸板沿虚线分割为八部分，再拼接成一个正方形，如图5所示，画出拼接示意图；若拼接后的正方形的面积为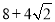
，则八角形纸板的边长为 ．
查看答案和解析>>
科目：初中数学 来源：2014年北京市西城区中考二模数学试卷（解析版） 题型：选择题
如图，为估算学校的旗杆的高度，身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去，当她走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC=2m，BC=8m，则旗杆的高度是（ ）
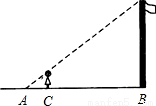
A．6.4m B．7m C．8m D．9 m
查看答案和解析>>
科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：解答题
已知关于
的方程：
①和
②，其中
.
（1）求证：方程①总有两个不相等的实数根；
（2）设二次函数
的图象与
轴交于
、
两点（点在点
的左侧），将
、两点按照相同的方式平移后，点
落在点
处，点
落在点
处，若点
的横坐标恰好是方程②的一个根，求
的值；
（3）设二次函数
，在（2）的条件下，函数
，
的图象位于直线
左侧的部分与直线
（
）交于两点，当向上平移直线时，交点位置随之变化，若交点间的距离始终不变，则
的值是________________.
查看答案和解析>>
科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：选择题
如图，四边形ABCD是⊙O的内接正方形，点P是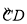
上不同于点C的任意一点，则∠BPC的大小是（ ）
A．45° B．60° C．75° D．90°
查看答案和解析>>
科目：初中数学 来源：2014年北京市怀柔区中考一模数学试卷（解析版） 题型：解答题
在平面直角坐标系xOy中，二次函数
的图象经过（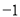
，0）和（
，0）两点.
（1）求此二次函数的表达式.
（2）直接写出当
＜x＜1时，y的取值范围.
（3）将一次函数 y=(1-m)x+2的图象向下平移m个单位后，与二次函数图象交点的横坐标分别是a和b,其中a<2<b，试求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
