练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，为估算学校的旗杆的高度，身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去，当她走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC=2m，BC=8m，则旗杆的高度是（　　）

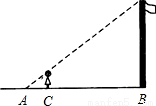
    A．6.4m B．7m C．8m D．9 m

     

    C.

    【解析】

    试题分析：因为人和旗杆均垂直于地面，所以构成相似三角形，利用相似比解题即可：

    设旗杆高度为h，

    由题意得，解得h=8 m．

    故选C．

    考点：相似三角形的应用．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2015届北京市丰台区八年级下学期期末考试数学试卷（解析版） 题型：选择题

    五边形的内角和为（ ）

    A．180° B．360° C．540° D．720°

     

    查看答案和解析>>

    科目：初中数学 来源：2014年江西省吉安市吉州区九年级下学期第一次中考模拟数学试卷（解析版） 题型：填空题

    已知线段AB＝10，点C是线段AB的黄金分割点（AC＞BC），则AC的长为_________。

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市西城区中考二模数学试卷（解析版） 题型：解答题

    已知关于的一元二次方程x2+2x+3k-6=0有两个不相等的实数根

    （1）求实数的取值范围；

    （2）若为正整数，且该方程的根都是整数，求的值．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市西城区中考二模数学试卷（解析版） 题型：填空题

    若一次函数的图像过点（0，2），且函数y随自变量x的增大而增大，请写出一个符合要求的一次函数表达式：_________

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：解答题

    对于半径为r的⊙P及一个正方形给出如下定义：若⊙P上存在到此正方形四条边距离都相等的点，则称⊙P是该正方形的“等距圆”．如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧.

    （1）当r=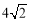时，

    ①在P1（0，-3），P2（4，6），P3（，2）中可以成为正方形ABCD的“等距圆”的圆心的是_______________；

    ②若点P在直线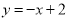上，且⊙P是正方形ABCD的“等距圆”，则点P的坐标为_______________；

    （2）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方.

    ①若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P 在y轴上截得的弦长；

    ②将正方形ABCD绕着点D旋转一周，在旋转的过程中，线段HF上没有一个点能成为它的“等距圆”的圆心，则r的取值范围是_______________．

     

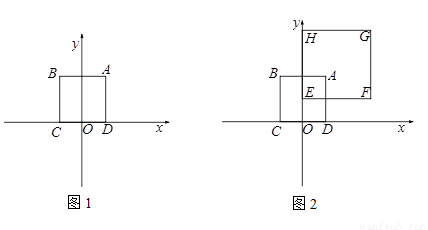
    查看答案和解析>>

    科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：解答题

    如图，一次函数的图象与反比例函数的图象交于点，与轴交于点.

    （1）求一次函数的解析式和点的坐标；

    （2）点C在x轴上，连接AC交反比例函数的图象于点P，且点P恰为线段AC的中点.请直接写出点P和点C的坐标.

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市海淀区中考二模数学试卷（解析版） 题型：选择题

    的相反数是（ ）

    A． B． C．-6 D．6

     

    查看答案和解析>>

    科目：初中数学 来源：2014年北京市房山区中考一模数学试卷（解析版） 题型：填空题

    分解因式：= ．

     

    查看答案和解析>>

    同步练习册答案