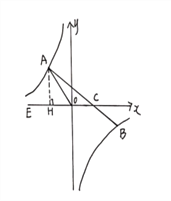
【题目】如图，在平面直角坐标系xoy中，一次函数y=kx+b（k≠0）的图象与反比例函数（m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（6，n）。线段OA=5，E为x轴上一点，且.

(1)求该反比例函数和一次函数的解析式；

(2)求△AOC的面积；

(3)直接写出一次函数值大于反比例函数自变量x的取值范围。

参考答案：

【答案】(1) y=; y=;(2)6;(3) x＜-3或0＜x＜6

【解析】试题分析：（1）过点A作AH⊥x轴于H点，由sin∠AOE=，OA=5，根据正弦的定义可求出AH，再根据勾股定理得到HO，即得到A点坐标（-3，4），把A（-3，4）代入y=，确定反比例函数的解析式；将B（6，n）代入，确定点B点坐标，然后把A点和B点坐标代入y=kx+b（k≠0），求出k和B即可；

（2）先令y=0，求出C点坐标，得到OC的长，然后根据三角形的面积公式计算△AOC的面积即可；

（3）观察图象可得当x＜-3或0＜x＜6时，反比例函数图象都在一次函数图象的下方，即一次函数值大于反比例函数值．

试题解析：（1）过A作AH⊥x轴交x轴于H，

∵sin∠ACE==，OA=5，

∴AH=4，∴OH= =3，

∴A（-3,4），

将A（-3，4）代入y=，得m=-12，∴反比例函数的解析式为y=- ，

将B（6，n）代入y=- ，得n=-2，

∴B（6，-2），

将A（-3，4）和B（6，-2）分别代入y=kx+b（k≠0），得 ，解得 ，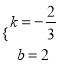

∴直线解析式：y= ；

(2)在直线y=中，令y=0，则有=0，解得x=3，

∴C（3,0），即OC=3，

∴；

(3)观察图象可得：当x＜-3或0＜x＜6时，一次函数值大于反比例函数值．

关闭