
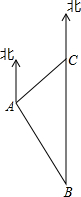
 海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
海上有两个灯塔B,C,其中灯塔C位于灯塔B的正北方向20海里处,在点A处测得灯塔C位于A的东北方向上,A位于灯塔B的北偏西30°方向上,点A与灯塔C之间的距离是多少?(结果精确到0.1海里.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 分析 作AD⊥BC于D,构建两个直角三角形,利用两个已知角的正切值求出AD的长,进而就可以求得AC的长.
解答 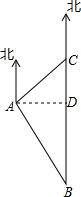 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
根据题意得:∠ABC=30°,∠CAD=45°,
在Rt△ABD中,BD=$\frac{AD}{tan30°}$=$\frac{AD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$AD,
在Rt△ACD中,CD=AD,
∵BC=BD+CD=$\sqrt{3}$AD+AD=20,
∴AD=10($\sqrt{3}$-1),
∴AC=$\sqrt{2}$AD=10$\sqrt{2}$($\sqrt{3}$-1)≈10.3海里.
答:点A与灯塔C之间的距离是10.3海里.
点评 此题主要考查了方向角问题的应用,根据已知得出△ADC为等腰直角三角形以及在直角三角形中求出AC的长是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:填空题
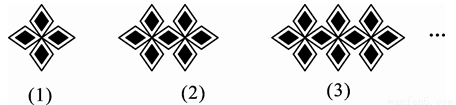
如图所示是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第n(n是正整数)个图案中的基础图形个数为________(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx-4的图象与y轴交于点C,与x轴的正半轴交于点A,且tan∠ACO=$\frac{1}{4}$.请解答下列问题:
已知二次函数y=x2+bx-4的图象与y轴交于点C,与x轴的正半轴交于点A,且tan∠ACO=$\frac{1}{4}$.请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
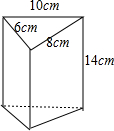 小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
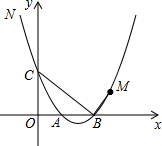 如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.
如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com