
 如图,已知∠A=∠B,OA=OB,AD与BC相交于点E,则OE平分∠AOB吗?说明理由.
如图,已知∠A=∠B,OA=OB,AD与BC相交于点E,则OE平分∠AOB吗?说明理由. 分析 要说明OE平分∠AOB,可证明△OCE≌△ODE或者△OAE≌△OBE.缺少边的条件,可通过证明△ACE≌△BDE获得.
解答 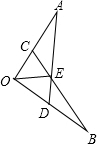 解:OE平分∠AOB.理由如下:
解:OE平分∠AOB.理由如下:
在△OAD和△OBC中,$\left\{\begin{array}{l}{∠A=∠B}\\{OA=OB}\\{∠AOB=∠BOA}\end{array}\right.$
∴△OAD≌△OBC(SAS)
∴OC=OD,
∴OA-OC=OB-OD,即AC=BD.
在△ACE和△BDE中,$\left\{\begin{array}{l}{∠AEC=∠BED}\\{∠A=∠B}\\{AC=BD}\end{array}\right.$
∴△ACE≌△BDE(AAS)
∴EC=ED
在△OCE和△ODE中,$\left\{\begin{array}{l}{OC=OD}\\{OE=OE}\\{CE=ED}\end{array}\right.$
∴△OCE≌△ODE(SSS)
∴∠COE=∠DOE,即OE平分∠AOB.
点评 本题考查了全等三角形的判定和性质.学会分析是关键.全等三角形的判定条件有四种:SSS,SAS,ASA,AAS.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.
如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,联结EC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 2008年第29届夏季奥林匹克运动会在北京举行,如图是奥林匹克运动会的五环标志,现在a,b,c,d,e,f,g,h,i之处分别填入1~9这9个整数中不同的一个,如果每一个环内的数字和都相等,记为M,则M的最大值是14.
2008年第29届夏季奥林匹克运动会在北京举行,如图是奥林匹克运动会的五环标志,现在a,b,c,d,e,f,g,h,i之处分别填入1~9这9个整数中不同的一个,如果每一个环内的数字和都相等,记为M,则M的最大值是14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰直角三角形ABC的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,请判断以x,a,b为边长的三角形的形状.
如图,等腰直角三角形ABC的斜边上取两点M,N,使∠MCN=45°,设AM=a,MN=x,BN=b,请判断以x,a,b为边长的三角形的形状.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com