
 如图,三张正方形纸片,面积分别为13cm2,29cm2和34cm2,将它们拼放在一起,中间恰好围成△ABC,求△ABC的面积.
如图,三张正方形纸片,面积分别为13cm2,29cm2和34cm2,将它们拼放在一起,中间恰好围成△ABC,求△ABC的面积. 分析 如图作边长为5cm的正方形NMPA,分成5×5的正方形网格,由勾股定理可知图中,△ABC的三边分别是三个正方形的边长,求出△ABC的面积即可.
解答 解: 因为13=32+22,29=52+22,34=52+32,如图作边长为5cm的正方形NMPA,分成5×5的正方形网格,
因为13=32+22,29=52+22,34=52+32,如图作边长为5cm的正方形NMPA,分成5×5的正方形网格,
由勾股定理可知图中,△ABC的三边分别是三个正方形的边长,
∴S△ABC=S正方形MNPA-S△AMB-S△BCN-S△APC
=25-$\frac{1}{2}$×5×2-$\frac{1}{2}$×3×2-$\frac{1}{2}$×5×3
=9.5.
∴△ABC的面积为9.5cm2.
点评 本题考查勾股定理,解题的关键是灵活运用勾股定理解决问题,学会利用网格图求三角形的面积,是数形结合的好题目,属于中考填空题中的压轴题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
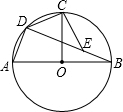 已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.
已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论:
在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、FA⊥AE交DP于点F,连接BF,FC.求证下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去
有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,△FGH的一个顶点F在y轴的负半轴上,射线FO平分∠GFH,过点H的直线MN交x轴于点M,满足∠MHF=∠GHN,过点H作HP⊥MN交x轴于点P,请探究∠MPH与∠G的数量关系,并写出简要证明思路.
如图,在平面直角坐标系xOy中,△FGH的一个顶点F在y轴的负半轴上,射线FO平分∠GFH,过点H的直线MN交x轴于点M,满足∠MHF=∠GHN,过点H作HP⊥MN交x轴于点P,请探究∠MPH与∠G的数量关系,并写出简要证明思路.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com