
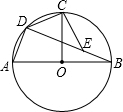
 已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.
已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.分析 (1)由条件可证明△ADC≌△BEC,则可得到CD=CE,结合AB为直径可证明∠DCE=90°,可判断△CDE为等腰直角三角形;
(2)由条件可证明△COD为等边三角形,则可求得CD=4,利用勾股定理可求得DE的长.
解答 解:
(1)△CDE为等腰直角三角形,
证明如下:
如图1,连接AC、BC,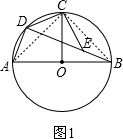
则∠DAC=∠DBC,
∵AB为直径,CO⊥AB,
∴△ABC为等腰直角三角形,
∴AC=BC,
在△ADC和△BEC中
$\left\{\begin{array}{l}{AD=BE}\\{∠DAC=∠EBC}\\{AC=BC}\end{array}\right.$
∴△ADC≌△BEC(SAS),
∴CD=CE,∠DCA=∠BCE,
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,
∴∠DCA+∠ACE=90°,即∠DCE=90°,
∴△CDE为等腰直角三角形;
(2)如图2,连接OD,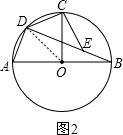
则∠AOD=2∠ABD=2×15°=30°,
∵∠AOC=90°,
∴∠DOC=60°,且OD=OC=OA=4,
∴△OCD为等边三角形,
∴CD=CE=OA=4,
在Rt△CDE中,由勾股定理可得DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
点评 本题主要考查全等三角形的判定和性质,构造全等三角形是解题的关键,在(2)中证明△OCD为等边三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O的半径为6,M是⊙O外一点,且OM=12,过M的直线与⊙O交于A、B,点A、B关于OM的对称点分别为C、D,AD与BC交于点P,则OP的长为( )
如图,已知⊙O的半径为6,M是⊙O外一点,且OM=12,过M的直线与⊙O交于A、B,点A、B关于OM的对称点分别为C、D,AD与BC交于点P,则OP的长为( )| A. | 4 | B. | 3.5 | C. | 3 | D. | 2.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.
九二班同学响应“每天锻炼一小时,幸福生活每一天”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑,跳绳,立定跳远,篮球定点定时投篮中任选一项进行训练,训练后进行了测试.现将项目选择人数机训练后篮球定时定点投篮球数进行整理,做出如下统计图表.| 进球(个数) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 2008年第29届夏季奥林匹克运动会在北京举行,如图是奥林匹克运动会的五环标志,现在a,b,c,d,e,f,g,h,i之处分别填入1~9这9个整数中不同的一个,如果每一个环内的数字和都相等,记为M,则M的最大值是14.
2008年第29届夏季奥林匹克运动会在北京举行,如图是奥林匹克运动会的五环标志,现在a,b,c,d,e,f,g,h,i之处分别填入1~9这9个整数中不同的一个,如果每一个环内的数字和都相等,记为M,则M的最大值是14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com