

分析 连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1,依题意可知△B1C1B2是等腰直角三角形,知道△B1B2D1与△C1AD1相似,求出相似比,根据三角形面积公式可得出S1,同理:B2B3:AC2=1:2,所以B2D2:D2C2=1:2,进而S2的值可求出,同样的道理,即可求出S3,S4…Sn的值.
解答 解:∵n+1个边长为1的等腰三角形有一条边在同一直线上,
∴S△AB1C1=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC
∵∠B1C1B2=$\frac{1}{2}$×90°=45°,
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=1,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$,
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3=$\frac{3}{4}$×$\frac{1}{2}$=$\frac{3}{8}$,
∴S4=$\frac{4}{5}$×$\frac{1}{2}$=$\frac{2}{5}$,
…
∴Sn=$\frac{n}{2(n+1)}$
故答案为:$\frac{1}{3}$;$\frac{n}{2(n+1)}$.
点评 本题主要考查相似三角形的判定和性质,等腰直角三角形的定义和性质、三角形的面公式等知识点、本题关键在于作好辅助线,得到相似三角形,求出相似比,就很容易得出答案了,意在提高同学们总结归纳的能力.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
 校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.
校园小记者就“端午节”知识随机采访了学校50名学生的情况统计图如下:A表示只知道吃粽子,B表示知道吃粽子和纪念屈原,C表示知道吃粽子、纪念屈原和悬挂药材驱瘟病,D表示知道吃粽子、纪念屈原、悬挂药材驱瘟病和赛龙舟.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )
如图,△ABC中,AB=AC,D为BC中点,在BA的延长线上取一点E,使得ED=EC,ED与AC交于点F,则$\frac{AF}{CF}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP,则BP的最大值是$\sqrt{13}$+2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.
如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
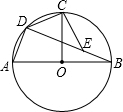 已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.
已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去
有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com