
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.

(1)求证:四边形AFCE为菱形;
(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.
(1)见解析 (2)a2=b2+c2
【解析】
分析:(1)由矩形ABCD与折叠的性质,易证得△CEF是等腰三角形,即CE=CF,即可证得AF=CF=CE=AE,即可得四边形AFCE为菱形.
(2)由折叠的性质,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之间的数量关系式为:a2=b2+c2.(答案不唯一)
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∴∠AEF=∠EFC.
由折叠的性质,可得:∠AEF=∠CEF,
AE=CE,AF=CF,∴∠EFC=∠CEF.
∴CF=CE.
∴AF=CF=CE=AE.
∴四边形AFCE为菱形.
(2)【解析】
a、b、c三者之间的数量关系式为:
a2=b2+c2.理由如下:
由折叠的性质,得:CE=AE.
∵四边形ABCD是矩形,∴∠D=90°.
∵AE=a,ED=b,DC=c,∴CE=AE=a.
在Rt△DCE中,CE2=CD2+DE2,
∴a、b、c三者之间的数量关系式可写为:a2=b2+c2.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源:2013-2014学年新人教版浙江永嘉桥下瓯渠中学中考数学总复习一练习卷(解析版) 题型:填空题
如图,数轴上的点P表示的数是-1,将点P向右移动3个单位长度得到点P′,则点P′表示的数是________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版浙江永嘉桥下瓯渠中学中考数学总复习一练习卷(解析版) 题型:选择题
如果零上5℃记作+5℃,那么零下7℃可记作 ( )
A.-7℃ B.+7℃
C.+12℃ D.-12℃
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版浙江永嘉桥下瓯渠中学中考数学总复习2练习卷(解析版) 题型:填空题
一个y关于x的函数同时满足两个条件:①图象过(2,1)点;②当x>0时.y随x的增大而减小,这个函数解析式为________(写出一个即可).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版浙江永嘉桥下瓯渠中学中考数学总复习2练习卷(解析版) 题型:选择题
如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是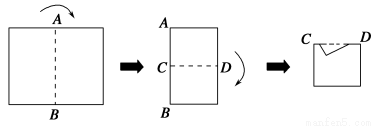

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版浙江永嘉桥下瓯渠中学中考数学总复习1练习卷(解析版) 题型:解答题
我市某工艺厂为配合奥运会,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价x(元/件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第四讲练习卷(解析版) 题型:解答题
分解因式:8(x2-2y2)-x(7x+y)+xy.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新人教版初中数学浙江永嘉桥下瓯渠中学中考总复习第十六讲练习卷(解析版) 题型:选择题
在平面直角坐标系中,将抛物线y=x2-x-6向上(下)或向左(右)平移m个单位,使平移后的抛物线恰好经过原点,则|m|的最小值为 ( )

A.1 B.2 C.3 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com