Question

△ABC中，已知∠BAC=15°，AD平分∠BAC，过A作DA的垂线交直线BC于M，若BM=AC+BA．求∠ABC、∠ACB的度数．

Answer 1

分析：此题应分两种情况讨论①当过A作AD的垂线交BC延长于点M时，延长BA到C，使AC′=AC，连接C′M，BM=AB+AC，根据各角的关系可得解．
②当过A作AD的垂线交CB延长线于点M时，延长BA到C′，使AC′=AC，连接CC′，C′M，BM=AB+AC，
根据三角形全等的性质得对应角的关系，求解即可．

解答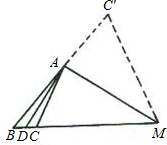：解：分两种情况讨论计算：
（1）当过A作AD的垂线交BC延长于点M时，延长BA到C，使AC′=AC，连接C′M（如图），则BM=AB+AC=AB+AC′=BC′
∴∠C′=∠C′MB，
已知AD平分∠BAC，AM⊥AD，
∴AM平分∠CAC′，
∴△ACM≌△AC′M（AAS），
∴∠AC′M=∠ACM=∠C′MB，
在△BC′M中，∠B+∠C′+∠C′MB=180°，
∴∠B+∠ACM+∠ACM=180°，
∴∠B+2（∠BAC+∠B）=180°，解得∠B=50°，
∴∠ACB=180°-∠B-∠BAC=115°；

（2）当过A作AD的垂线交CB延长线于点M时，
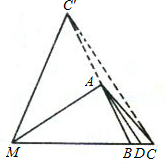
延长BA到C′，使AC′=AC，连接CC′，C′M（如图），
则BM=AB+AC=AB+AC′=BC′，
∴∠MC′A=∠MBA，
∵∠MAD=90°，∴∠MAC=90°+

∠BAC

2

=97.5°，
又∵∠C′AC=180°-∠BAC=165°，
∴∠C′AM=360°-∠CAC′-∠MAC=97.5°=∠CAM，
∵AM=AM，
∴△AC′M≌△ACM（SAS），
∴∠AC′M=∠ACB，
在△MC′C中，∠C′MB+∠MCC′+∠MCC′=180°，
∴∠MC′A+∠MCA+∠ACC′+∠MC′A+∠AC′C=180°，
∴3∠ACM+∠CAB=180°，
∴∠ACB=

1

3

（180°-15°）=55°，
∴∠ABC=180°-∠ACB-∠BAC=110°，
综上得∠ABC=50°，∠ACB=115°或∠ABC=110°，∠ACB=55°．

点评：本题考查了三角形全等的判定和性质，涉及到三角形内角和定理、角平分线的性质等知识点．理解题意正确作出图形及辅助线是解题的关键．