
【题目】如图,反比例函数y= ![]() (x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( )
(x>0)的图象与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,若OC=2BD,则实数k的值为( ) 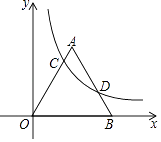
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F, 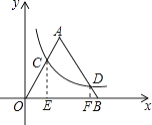
设OC=2x,则BD=x,
在Rt△OCE中,∠COE=60°,
则OE=x,CE= ![]() x,
x,
则点C坐标为(x, ![]() x),
x),
在Rt△BDF中,BD=x,∠DBF=60°,
则BF= ![]() x,DF=
x,DF= ![]() x,
x,
则点D的坐标为(5﹣ ![]() x,
x, ![]() x),
x),
将点C的坐标代入反比例函数解析式可得:k= ![]() x2 ,
x2 ,
将点D的坐标代入反比例函数解析式可得:k= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
则 ![]() x2=
x2= ![]() x﹣
x﹣ ![]() x2 ,
x2 ,
解得:x1=2,x2=0(舍去),
故k= ![]() x2=
x2= ![]() ×4=4
×4=4 ![]() .
.
故选A.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2= ![]() 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0). 
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分别绕直线AB,CD旋转一周,所得几何体的表面积分别为S1 , S2 , 则|S1﹣S2|=(平方单位) 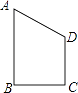
查看答案和解析>>
科目:初中数学 来源: 题型:
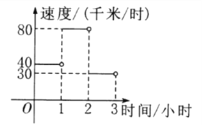
【题目】某人驾车从乡村进城.各时间段的行驶速度如图所示.当![]() 时,其行驶路程
时,其行驶路程![]() 与时间
与时间![]() 之间的函数表达式是________,当
之间的函数表达式是________,当![]() 时,其行驶路程
时,其行驶路程![]() 与时间
与时间![]() 之间的函数表达式是________,当
之间的函数表达式是________,当![]() 时,其行驶路程
时,其行驶路程![]() 与时间
与时间![]() 之间的函数表达式是________.
之间的函数表达式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= ![]() .
.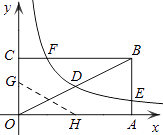
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格线的交点叫格点,格点P是∠AOB的边OB上的一点(请利用网格作图,保留作图痕迹). 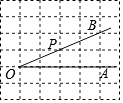
(1)过点P画OB的垂线,交OA于点C;
(2)线段的长度是点O到PC的距离;
(3)PC<OC的理由是;
(4)过点C画OB的平行线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为开展体育大课间活动,需要购买篮球与足球若干个.已知购买2个篮球和3个足球共需要380元;购买4个篮球和5个足球共需要700元.
(1)求购买一个篮球、一个足球各需多少元?
(2)若体育老师带了6000元去购买这种篮球与足球共80个.由于数量较多,店主给出“一律打九折”的优惠价,那么他最多能购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com