
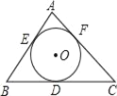
【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF=______.
【答案】50°或130°
【解析】
有两种情况:①当P在弧EDF上时,连接OE、OF,求出∠EOF,根据圆周角定理求出即可;②当P在弧EMF上时,∠EPF=∠EMF,根据圆内接四边形的性质得到∠EMF+∠ENF=180°,代入求出即可.
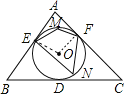
有两种情况:
①当P在弧EDF上时,∠EPF=∠ENF,连接OE、OF,
∵圆O是△ABC的内切圆,∴OE⊥AB,OF⊥AC,∴∠AEO=∠AFO=90°,
∵∠A=80°,∴∠EOF=360°∠AEO∠AFO∠A=100°,∴∠ENF=∠EPF=![]() ∠EOF=50°,
∠EOF=50°,
②当P在弧EMF上时,∠EPF=∠EMF,∠FPE=∠FME=180°50°=130°.
故答案为:50°或130°.


科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年国内生产总值(GDP)比2016年增长了12%,由于受到国际金融危机的影响,预计2018比2017年增长7%,若这两年GDP年平均增长率为![]() %,则
%,则![]() %满足的关系是( )
%满足的关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
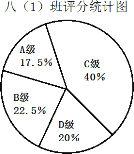

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘一名员工,现有甲、乙两人竞聘,公司聘请了3位专家和4位群众代表组成评审组,评审组对两人竟聘演讲进行现场打分,记分采用100分制,其得分如下表:
评委(序号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
甲(得分) | 89 | 94 | 93 | 87 | 95 | 92 | 87 |
乙(得分) | 87 | 89 | 91 | 95 | 94 | 96 | 89 |
(1)甲、乙两位竞聘者得分的中位数分别是多少
(2)计算甲、乙两位应聘者平均得分,从平均得分看应该录用谁(结果保留一位小数)
(3)现知道1、2、3号评委为专家评委,4、5、6、7号评委为群众评委,如果对专家评委组与群众评委组的平均分数分别赋子适当的权,那么对专家评委组赋的权至少为多少时,甲的平均得分比乙的平均得分多0.5分及以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).


查看答案和解析>>
科目:初中数学 来源: 题型:
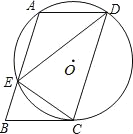
【题目】如图,在ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
(1)求证:AD=CE;
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若BC=4,DE=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
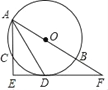
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:设a+b
)2.善于思考的小明进行了以下探索:设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为整数),则有a+b
)2(其中a,b,m,n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a=______________,b=________;
)2,用含m,n的式子分别表示a,b,得a=______________,b=________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:
________+________![]() =(________+________
=(________+________![]() )2;
)2;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
(4)试化简![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com