
【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数对应的点沿数轴向右平移
,再把所得数对应的点沿数轴向右平移![]() 个单位长度,得到点
个单位长度,得到点![]() .称这样的操作为点
.称这样的操作为点![]() 的“倍移”,对数轴上的点
的“倍移”,对数轴上的点![]() ,
,![]() ,
, ![]() ,
,![]() 进行“倍移”操作得到的点分别为
进行“倍移”操作得到的点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,
时,
①若点![]() 表示的数为
表示的数为![]() ,则它的对应点
,则它的对应点![]() 表示的数为 .若点
表示的数为 .若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数为 ; ②数轴上的点
表示的数为 ; ②数轴上的点![]() 表示的数为1,若
表示的数为1,若![]() ,则点
,则点![]() 表示的数为 ;
表示的数为 ;
(2)当![]() 时,若点
时,若点![]() 表示的数为
表示的数为![]() ,则
,则![]() 的值为 ;
的值为 ;
(3)若线段![]() ,请写出你能由此得到的结论.
,请写出你能由此得到的结论.
【答案】(1)① ![]() ;
;![]() ; ②
; ② ![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 等
等
【解析】
(1)①根据题目规定以及数轴上的数向右平移用加法计算即可求出点![]() ,设点B表示的数为a,根据题意列出方程求解即可得到点B表示的数;
,设点B表示的数为a,根据题意列出方程求解即可得到点B表示的数;
②设点C表示的数为b,根据“倍移”规律得到点![]() 表示的数为
表示的数为![]() ,从而可表示出CM,
,从而可表示出CM,![]() M,根据
M,根据![]() 列方程求解即可得到答案;
列方程求解即可得到答案;
(2)根据“倍移”规律列方程求解即可;
(3)设A点表示的数为x,B点表示的数为y,则![]() 表示的数为mx+n,
表示的数为mx+n,![]() 表示的数为my+n,
表示的数为my+n,
根据![]() 列方程求解即可.
列方程求解即可.
(1)①点A′:![]() ;
;
设点B表示的数为a,根据题意得:![]()
解得,a=4,
∴点![]() 表示的数为:4;
表示的数为:4;
②设点C表示的数为b,
所以,点![]() 表示的数为:
表示的数为:![]() ,
,
∵点![]() 表示的数为1,
表示的数为1,
∴CM=|b-1|,![]() ,
,
∵![]() ,
,
∴|b-1|=3|![]() |
|
∴![]() ,
,
解得:b=-2或b=![]() ,
,
故C点表示的数为:b=-2或b=![]() ;
;
(2)根据题意得,![]() ,
,
解得,m=-4;
(3)设A点表示的数为x,B点表示的数为y,则![]() 表示的数为mx+n,
表示的数为mx+n,![]() 表示的数为my+n,
表示的数为my+n,
∴AB=|x-y|,![]()
∵![]()
∴![]()
∴![]() ,
,
∴m=±2.


科目:初中数学 来源: 题型:
【题目】如果关于![]() 的不等式组
的不等式组![]() 的整数解仅有
的整数解仅有![]() ,
,![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有_______个;如果关于
共有_______个;如果关于![]() 的不等式组
的不等式组![]() (其中
(其中![]() ,
,![]() 为正整数)的整数解仅有
为正整数)的整数解仅有![]() ,那么适合这个不等式组的整数
,那么适合这个不等式组的整数![]() ,
,![]() 组成的有序数对
组成的有序数对![]() 共有______个.(请用含
共有______个.(请用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求平行四边形ACDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
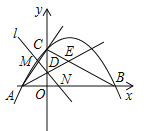
【题目】(2017南宁,第26题,10分)如图,已知抛物线![]() 与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l与射线AC,AB分别交于点M,N.
(1)直接写出a的值、点A的坐标及抛物线的对称轴;
(2)点P为抛物线的对称轴上一动点,若△PAD为等腰三角形,求出点P的坐标;
(3)证明:当直线l绕点D旋转时,![]() 均为定值,并求出该定值.
均为定值,并求出该定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
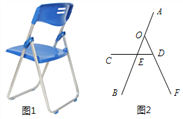
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示.若座板CD平行于地面,前支撑架AB与后支撑架OF分别与CD交于点E、D,ED= 15㎝,OD=20㎝,DF=40㎝,∠ODC=60°,∠AED=50°.
(1)求两支架着地点B、F之间的距离;
(2)若A、D两点所在的直线正好与地面垂直,求椅子的高度(结果取整数).
(参考数据: ![]()
![]() ;可使用科学计算器.)
;可使用科学计算器.)
查看答案和解析>>
科目:初中数学 来源: 题型:
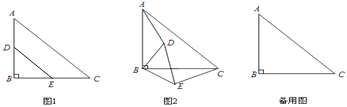
【题目】如图1,△DBE和△ABC都是等腰直角三角形,D,E两点分别在AB,BC上,∠B=90°.将△DBE绕点B顺时针旋转,得到图2.
(1)在图2中,求证:AD=CE;
(2)设AB= ![]() ,BD=
,BD= ![]() ,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和
,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y1=x+2与反比例函数y2=![]() (x>0)的图象交于点A(a,5)
(x>0)的图象交于点A(a,5)
(1)确定反比例函数的表达式;
(2)结合图象,直接写出x为何值时,y1<y2
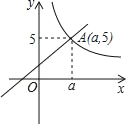
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com