
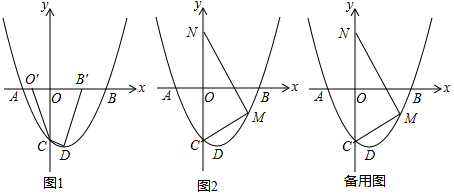
���� ��1����y=0���ⷽ�̼��������A��B�����꣬�����䷽�������깫ʽ�ɵö���D�����ꣻ
��2������C��0��-3������x��ĶԳƵ�C�䣨0��3��������C�䣨0��3������ƽ��4����λ�õ���C�壨4��3��������DC�壬��x���ڵ�B�䣬����B������ƽ��4����λ�õ���O�䣬����CO�䣬CO�壬���ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ���ٸ��������ľ��빫ʽ���CD��DC��ij��ȣ����ɵó����ۣ�
��3������M��λ�ò�ͬ������������ǣ��ٵ�M��ֱ��y=x-3�ϣ����ڵ�M��ֱ��y=-x-3�ϣ�����ֱ���������߽���ʽ�����M�����꣬��ϵ�C�������Լ�����ֱ�������ε����ʼ��ɵó���N�����꣮�ۺ�����������ɵó����ۣ�
��� �⣺��1����y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��y=0���� $\frac{3}{8}$x2-$\frac{3}{4}$x-3=0��
��ã�x1=-2��x2=4��
��A��-2��0����B��4��0����
��y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3=$\frac{3}{8}$��x2-2x��-3=$\frac{3}{8}$��x-1��2-$\frac{27}{8}$��
��D��1��-$\frac{27}{8}$����
��2����y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3��x=0����y=-3��
��C��0��-3����
D��1��-$\frac{27}{8}$����O��B��=OB=4��
��ͼ1������C��0��-3������x��ĶԳƵ�C�䣨0��3��������C�䣨0��3������ƽ��4����λ�õ���C�壨4��3��������DC�壬��x���ڵ�B�䣬����B������ƽ��4����λ�õ���O�䣬����CO�䣬CO�壬���ı���O��B��C��C��Ϊƽ���ı��Σ���ʱ�ı���O��B��DC�ܳ�ȡ��Сֵ��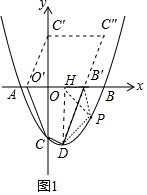
��ʱC�ı���O��B��DC=CD+O��B��+CO��+DB��=CD+OB��+DC�壮
��O��B��=4��CD=$\sqrt{��1-0��^{2}+��-3+\frac{27}{8}��^{2}}$=$\frac{\sqrt{73}}{8}$��C��D=$\sqrt{��4-1��^{2}+��3+\frac{27}{8}��^{2}}$=$\frac{3\sqrt{353}}{8}$��
���ı���O��B��DC���ܳ���СֵΪ4+$\frac{\sqrt{73}}{8}$+$\frac{3\sqrt{353}}{8}$��
��P��m��$\frac{3}{8}$m2-$\frac{3}{4}$m-3������DH��x����H������PH����֪H��1��0����B�䣨$\frac{44}{17}$��0��
S��PDB��=S��PDH+S��PHB��-S��DHB��=$\frac{1}{2}$•$\frac{27}{8}$��m-1��+$\frac{1}{2}$•$\frac{27}{17}$•��-$\frac{3}{8}$m2+$\frac{3}{4}$m+3��-$\frac{1}{2}$•$\frac{27}{8}$•$\frac{27}{17}$
=$\frac{27}{272}$��-3m2+23m-20����
��m=$\frac{23}{6}$ʱ����PDB���������
��ʱP��$\frac{23}{6}$��-$\frac{37}{96}$����
��3����CMN����MNΪֱ�DZߵĵ���ֱ�������η������������ͼ2����
�ٹ���C��ֱ��y=x-3���������ڵ�M��
����ֱ��CM�������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{y=x-3}\\{y=\frac{3}{8}{x}^{2}-\frac{3}{4}x-3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=\frac{14}{3}}\\{y=\frac{5}{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$��
��M�� $\frac{14}{3}$��$\frac{5}{3}$����
�ߡ�CMNΪ����ֱ�������Σ�C��0��-3����
���N��������0��$\frac{5}{3}$����0��$\frac{19}{3}$����
�ڹ���C��ֱ��y=-x-3���������ڵ�M��
����ֱ��CM�������ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{y=-x-3}\\{y=\frac{3}{8}{x}^{2}-\frac{3}{4}x-3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=-\frac{7}{3}}\end{array}\right.$�� $\left\{\begin{array}{l}{x=0}\\{y=-3}\end{array}\right.$��
��M��-$\frac{2}{3}$��-$\frac{7}{3}$����
�ߡ�CMNΪ����ֱ�������Σ�C��0��-3����
���N��������0��-$\frac{7}{3}$����0��-$\frac{5}{3}$����
���Ͽ�֪������CMN����MNΪֱ�DZߵĵ���ֱ��������ʱ����N������Ϊ��0��$\frac{5}{3}$������0��$\frac{19}{3}$������0��-$\frac{7}{3}$����0��-$\frac{5}{3}$����
���� ���⿼����κ����ۺ��⡢һԪ���η��̡�����ֱ�������ε������Լ���Ԫ���η������֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�����öԳƽ��������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ��O�ཻ�ڵ�D����֤��DE=DB��
��ͼ����E�ǡ�ABC�����ģ�AE���ӳ��ߺ͡�ABC�����Բ��O�ཻ�ڵ�D����֤��DE=DB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
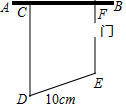 �Ŵ�����һ�¾�ǽAB���ó�50m�����Χ��һ������1m�����ŵ����γ���CDEF��CD��EF������ͼ��ʾ����DE�ij�Ϊ10m�������γ���CDEF���������Ƕ��٣�
�Ŵ�����һ�¾�ǽAB���ó�50m�����Χ��һ������1m�����ŵ����γ���CDEF��CD��EF������ͼ��ʾ����DE�ij�Ϊ10m�������γ���CDEF���������Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
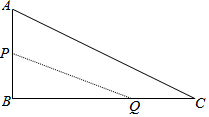 ��ͼ���ڡ�ABC�У���B=90�㣬AB=6mm��BC=12mm������P�ӵ�A��ʼ�ر�AB���B��1mm/s���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC���C��2mm/s���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ��������ô����3�룬�ı���APQC�������С��
��ͼ���ڡ�ABC�У���B=90�㣬AB=6mm��BC=12mm������P�ӵ�A��ʼ�ر�AB���B��1mm/s���ٶ��ƶ��������B�غϣ�������Q�ӵ�B��ʼ�ر�BC���C��2mm/s���ٶ��ƶ��������C�غϣ������P��Q�ֱ��A��Bͬʱ��������ô����3�룬�ı���APQC�������С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| һ������һ�����õ����ķ�Χ | ��Ѽ۸�λ��Ԫ/ǧ��ʱ�� |
| ������150ǧ��ʱ | a |
| ����150ǧ��ʱ��������300ǧ��ʱ�IJ��� | 0.65 |
| ����300ǧ��ʱ�IJ��� | 0.9 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com