
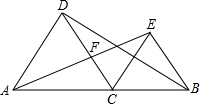
 如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE,则EF等于$\frac{{b}^{4}}{{a}^{3}}$.
如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE,则EF等于$\frac{{b}^{4}}{{a}^{3}}$. 分析 依次判定△ABC∽△BDC∽△CDE∽△DFE,根据相似三角形的对应边成比例的知识,可得出EF的长度.
解答 解:∵AB=AC,
∴∠ABC=∠ACB,
又∵∠CBD=∠A,
∴△ABC∽△BDC,
同理可得:△ABC∽△BDC∽△CDE∽△DFE,
∴$\frac{AB}{BC}=\frac{BC}{CD}$,$\frac{CD}{BD}=\frac{DE}{CD}$,$\frac{AB}{CD}=\frac{AC}{CE}$,$\frac{EF}{DE}=\frac{DE}{CE}$,
∵AB=AC,
∴CD=CE,
解得:CD=CE=$\frac{{b}^{2}}{a}$,DE=$\frac{{b}^{3}}{{a}^{2}}$,EF=$\frac{{b}^{4}}{{a}^{3}}$.
故答案为:$\frac{{b}^{4}}{{a}^{3}}$.
点评 本题考查了相似三角形的判定与性质,本题中相似三角形比较容易找到,难点在于根据对应边成比例求解线段的长度,注意仔细对应,不要出错.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )
我市正在进行轻轨九号线的建设,为了缓解市区一些主要路段的交通拥堵现状,交警大队在主要路口设置了交通路况指示牌如图所示,小明在离指示牌3米的点A处测得指示牌顶端D点和底端E点的仰角分别为60°和30°,则路况指示牌DE的高度为( )| A. | 3-$\sqrt{3}$ | B. | 2$\sqrt{3}$-3 | C. | 2$\sqrt{3}$ | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-3,-3) | B. | (-2,-2) | C. | (-1,-3) | D. | (0,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )| A. | △ABD∽△ACE | B. | ∠B=∠C | C. | BD=2CE | D. | AB•EC=AC•BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10),请你结合表格和图象:| 付款金额 | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com