Question

【题目】如图，MN是⊙O的直径，QN是⊙O的切线，连接MQ交⊙O于点H，E为上一点，连接ME，NE，NE交MQ于点F，且ME2=EFEN．

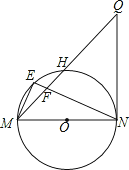
（1）求证：QN=QF；

（2）若点E到弦MH的距离为1，cos∠Q=，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）2.5．

【解析】

试题分析：（1）如图1，通过相似三角形（△MEF∽△MEN）的对应角相等推知，∠1=∠EMN；又由弦切角定理、对顶角相等证得∠2=∠3；最后根据等角对等边证得结论；

（2）如图2，连接OE交MQ于点G，设⊙O的半径是r．根据（1）中的相似三角形的性质证得∠EMF=∠ENM，所以由“圆周角、弧、弦间的关系”推知点E是弧MH的中点，则OE⊥MQ；然后通过解直角△MNE求得cos∠Q=sin∠GMO=，则可以求r的值．

试题解析：（1）如图1，

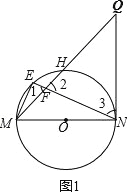
∵ME2=EFEN，

∴．

又∵∠MEF=∠MEN，

∴△MEF∽△MEN，

∴∠1=∠EMN．

∵∠1=∠2，∠3=∠EMN，

∴∠2=∠3，

∴QN=QF；

（2）解：如图2，连接OE交MQ于点G，设⊙O的半径是r．

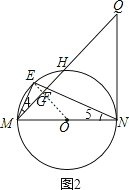
由（1）知，△MEF∽△MEN，则∠4=∠5．

∴．

∴OE⊥MQ，

∴EG=1．

∵cos∠Q=，且∠Q+∠GMO=90°，

∴sin∠GMO=，

∴，即，

解得，r=2.5，即⊙O的半径是2.5．