
ЮЊСЫСЫНтбЇЩњдквЛФъжаЕФПЮЭтдФЖССПЃЌОХЃЈ1ЃЉАрЖдОХФъМЖ800УћбЇЩњВЩгУЫцЛњГщбљЕФЗНЪННјааСЫЮЪОэЕїВщЃЌЕїВщЕФНсЙћЗжЮЊЫФжжЧщПіЃКAЃЎ10БОвдЯТЃЛB.10ЁЋ15БОЃЛC.16ЁЋ20БОЃЛD.20БОвдЩЯЃЎИљОнЭГМЦећРэВЂжЦзїСЫШчЭМЫљЪОЕФСНЗљЭГМЦЭМБэЃК
ЃЈ1ЃЉдкетДЮЕїВщжавЛЙВГщВщСЫЁЁ ЁЁУћбЇЩњЃЛ
ЃЈ2ЃЉБэжаxЃЌyЕФжЕЗжБ№ЮЊЃКx= ЃЌy= ЁЁЃЛ
ЃЈ3ЃЉдкЩШаЮЭГМЦЭМжаЃЌCВПЗжЫљЖдгІЕФЩШаЮЕФдВаФНЧЪЧЁЁЁЁ ЖШЃЛ
ЃЈ4ЃЉИљОнГщбљЕїВщНсЙћЃЌЧыЙРМЦОХФъМЖбЇЩњвЛФъдФЖСПЮЭтЪщ20БОвдЩЯЕФбЇЩњШЫЪ§ЃЎ


(1)200; (2)60ЃЌ80ЃЛЃЈ3ЃЉ144ЃЛЃЈ4ЃЉ160.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУAВПЗжЕФШЫЪ§ЁТAВПЗжШЫЪ§ЫљеМАйЗжБШМДПЩЫуГіБОДЮЮЪОэЕїВщЙВГщШЁЕФбЇЩњЪ§ЃЛ
ЃЈ2ЃЉx=ГщВщЕФбЇЩњзмЪ§ЁСBВПЗжЕФбЇЩњЫљеМАйЗжБШЃЌy=ГщВщЕФбЇЩњзмЪ§ЉAВПЗжЕФШЫЪ§ЉBВПЗжЕФШЫЪ§ЉDВПЗжЕФШЫЪ§ЃЛ
ЃЈ3ЃЉCВПЗжЫљЖдгІЕФЩШаЮЕФдВаФНЧЕФЖШЪ§=360ЁуЁСЫљеМАйЗжБШЃЛ
ЃЈ4ЃЉРћгУбљБОЙРМЦзмЬхЕФЗНЗЈЃЌгУ800ШЫЁСЕїВщЕФбЇЩњжавЛФъдФЖСПЮЭтЪщ20БОвдЩЯЕФбЇЩњШЫЪ§ЫљеМАйЗжБШЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ20ЁТ10%=200ЃЈШЫЃЉЃЌ
дкетДЮЕїВщжавЛЙВГщВщСЫ200УћбЇЩњЃЌ
ЃЈ2ЃЉx=200ЁС30%=60ЃЌy=200Љ20Љ60Љ40=80ЃЌ
ЃЈ3ЃЉ360ЁС =144ЁуЃЌ
=144ЁуЃЌ
CВПЗжЫљЖдгІЕФЩШаЮЕФдВаФНЧЪЧ144ЖШЃЌ
ЃЈ4ЃЉ800ЁС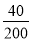 =160ЃЈШЫЃЉЃЎ
=160ЃЈШЫЃЉЃЎ
ПМЕуЃК1.ЦЕЪ§ЃЈТЪЃЉЗжВМБэЃЛ2.гУбљБОЙРМЦзмЬхЃЛ3.ЩШаЮЭГМЦЭМ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯЩлбєОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
вбжЊЁЯІС=13ЁуЃЌдђЁЯІСЕФгрНЧДѓаЁЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯЯцЬЖОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
вбжЊСНжБЯпL1ЃКy=k1x+b1ЃЌL2ЃКy=k2x+b2ЃЌШєL1ЁЭL2ЃЌдђгаk1•k2=Љ1ЃЎ
ЃЈ1ЃЉгІгУЃКвбжЊy=2x+1гыy=kxЉ1ДЙжБЃЌЧѓkЃЛ
ЃЈ2ЃЉжБЯпОЙ§AЃЈ2ЃЌ3ЃЉЃЌЧвгыy= x+3ДЙжБЃЌЧѓНтЮіЪНЃЎ
x+3ДЙжБЃЌЧѓНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯЯцЬЖОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
вдЯТЫФИіУќЬте§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
AЃЎШЮвтШ§ЕуПЩвдШЗЖЈвЛИідВ
BЃЎСтаЮЖдНЧЯпЯрЕШ
CЃЎжБНЧШ§НЧаЮаББпЩЯЕФжаЯпЕШгкаББпЕФвЛАы
DЃЎЦНааЫФБпаЮЕФЫФЬѕБпЯрЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯгРжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ШчЭМЃЌХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ2ЃЉЃЌЕуMЃЈmЃЌnЃЉЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЮЛгкЖдГЦжсЕФзѓВрЃЌВЂЧвВЛдкзјБъжсЩЯЃЌЙ§ЕуMзїxжсЕФЦНааЯпНЛyжсгкЕуQЃЌНЛХзЮяЯпгкСэвЛЕуEЃЌжБЯпBMНЛyжсгкЕуFЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіЦфЖЅЕузјБъЃЛ
ЃЈ2ЃЉЕБSЁїMFQЃКSЁїMEB=1ЃК3ЪБЃЌЧѓЕуMЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯгРжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
ШчЭМЃЌвбжЊжБЯпl1ЃКy=k1x+4гыжБЯпl2ЃКy=k2xЉ5НЛгкЕуAЃЌЫќУЧгыyжсЕФНЛЕуЗжБ№ЮЊЕуBЃЌCЃЌЕуEЃЌFЗжБ№ЮЊЯпЖЮABЁЂACЕФжаЕуЃЌдђЯпЖЮEFЕФГЄЖШЮЊ ЁЁЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯгРжнОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКбЁдёЬт
дкЧѓ1+62+63+64+65+66+67+68+69ЕФжЕЪБЃЌаЁСжЗЂЯжЃКДгЕкЖўИіМгЪ§Ц№УПвЛИіМгЪ§ЖМЪЧЧАвЛИіМгЪ§ЕФ6БЖЃЌгкЪЧЫ§ЩшЃК
S=1+62+63+64+65+66+67+68+69Ђй
ШЛКѓдкЂйЪНЕФСНБпЖМГЫвд6ЃЌЕУЃК
6S=6+62+63+64+65+66+67+68+69+610Ђк
ЂкЉЂйЕУ6SЉS=610Љ1ЃЌМД5S=610Љ1ЃЌЫљвдS= ЃЌЕУГіД№АИКѓЃЌАЎЖЏФдНюЕФаЁСжЯыЃК
ЃЌЕУГіД№АИКѓЃЌАЎЖЏФдНюЕФаЁСжЯыЃК
ШчЙћАбЁА6ЁБЛЛГЩзжФИЁАaЁБЃЈaЁй0ЧвaЁй1ЃЉЃЌФмЗёЧѓГі1+a+a2+a3+a4+Ё+a2014ЕФжЕЃПФуЕФД№АИЪЧЃЈЁЁЁЁЃЉ
AЃЎ BЃЎ
BЃЎ CЃЎ
CЃЎ DЃЎa2014Љ1
DЃЎa2014Љ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯжъжоОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКЬюПеЬт
жБЯпy=k1x+b1ЃЈk1ЃО0ЃЉгыy=k2x+b2ЃЈk2ЃМ0ЃЉЯрНЛгкЕуЃЈЉ2ЃЌ0ЃЉЃЌЧвСНжБЯпгыyжсЮЇГЧЕФШ§НЧаЮУцЛ§ЮЊ4ЃЌФЧУДb1Љb2ЕШгкЁЁ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2014ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКўФЯдРбєОэЃЉЪ§бЇЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ШчЭМЃЌХзЮяЯпОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ ЃЉШ§ЕуЃЌЩшЕуEЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЧвдкxжсЯТЗНЃЌЫФБпаЮOEBFЪЧвдOBЮЊЖдНЧЯпЕФЦНааЫФБпаЮЃЎ
ЃЉШ§ЕуЃЌЩшЕуEЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЧвдкxжсЯТЗНЃЌЫФБпаЮOEBFЪЧвдOBЮЊЖдНЧЯпЕФЦНааЫФБпаЮЃЎ
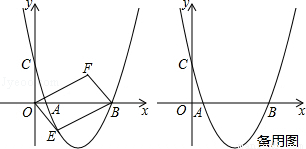
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуEЃЈxЃЌyЃЉдЫЖЏЪБЃЌЪдЧѓЦНааЫФБпаЮOEBFЕФУцЛ§SгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіУцЛ§SЕФзюДѓжЕЃП
ЃЈ3ЃЉЪЧЗёДцдкетбљЕФЕуEЃЌЪЙЦНааЫФБпаЮOEBFЮЊе§ЗНаЮЃПШєДцдкЃЌЧѓEЕуЃЌFЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com