
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)当S△MFQ:S△MEB=1:3时,求点M的坐标.

(1)y=﹣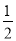 x2+
x2+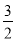 x+2,顶点坐标为(
x+2,顶点坐标为(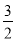 ,
,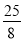 );(2)(1,3)或(﹣12,﹣88).
);(2)(1,3)或(﹣12,﹣88).
【解析】
试题分析:(1)把点A、B、C的坐标代入抛物线解析式得到关于a、b、c的三元一次方程组,然后求解即可,再把函数解析式整理成顶点式形式,然后写出顶点坐标;
(2)根据点M的坐标表示出点Q、E的坐标,再设直线BM的解析式为y=kx+b(k≠0),然后利用待定系数法求出一次函数解析式,再求出点F的坐标,然后求出MQ、FQ、ME,再表示出△MFQ和△MEB的面积,然后列出方程并根据m的取值范围整理并求解得到m的值,再根据点M在抛物线上求出n的值,然后写出点M的坐标即可.
试题解析:(1)∵抛物线y=ax2+bx+c过点A(﹣1,0),B(4,0),C(0,2),
∴ ,
,
解得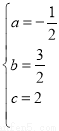 ,
,
∴y=﹣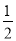 x2+
x2+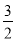 x+2,
x+2,
∵y=﹣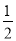 x2+
x2+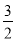 x+2=﹣
x+2=﹣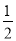 (x2﹣3x+
(x2﹣3x+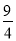 )+
)+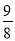 +2=﹣
+2=﹣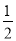 (x﹣
(x﹣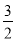 )2+
)2+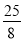 ,
,
∴顶点坐标为(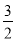 ,
,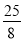 );
);
(2)∵M(m,n),
∴Q(0,n),E(3﹣m,n),
设直线BM的解析式为y=kx+b(k≠0),
把B(4,0),M(m,n)代入得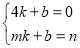 ,
,
解得 ,
,
∴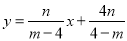 ,
,
令x=0,则y=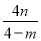 ,
,
∴点F的坐标为(0,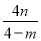 ),
),
∴MQ=|m|,FQ=|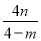 ﹣n|=|
﹣n|=|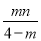 |,ME=|3﹣m﹣m|=|3﹣2m|,
|,ME=|3﹣m﹣m|=|3﹣2m|,
∴S△MFQ=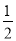 MQ•FQ=
MQ•FQ=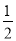 |m|•|
|m|•|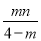 |=
|=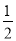 |
|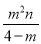 |,
|,
S△MEB=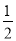 ME•|n|=
ME•|n|=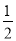 •|3﹣2m|•|n|,
•|3﹣2m|•|n|,
∵S△MFQ:S△MEB=1:3,
∴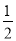 |
|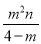 |×3=
|×3=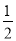 •|3﹣2m|•|n|,
•|3﹣2m|•|n|,
即|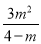 |=|3﹣2m|,
|=|3﹣2m|,
∵点M(m,n)在对称轴左侧,
∴m<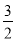 ,
,
∴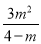 =3﹣2m,
=3﹣2m,
整理得,m2+11m﹣12=0,
解得m1=1,m2=﹣12,
当m1=1时,n1=﹣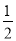 ×12+
×12+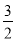 ×1+2=3,
×1+2=3,
当m2=﹣12时,n2=﹣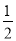 ×(﹣12)2+
×(﹣12)2+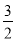 ×(﹣12)+2=﹣88,
×(﹣12)+2=﹣88,
∴点M的坐标为(1,3)或(﹣12,﹣88).
考点:二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(湖南邵阳卷)数学(解析版) 题型:填空题
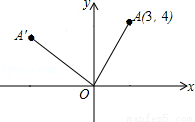
如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南衡阳卷)数学(解析版) 题型:选择题
环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
A.2.5×10﹣5 B.2.5×105 C.2.5×10﹣6 D.2.5×106
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:解答题
为了了解学生在一年中的课外阅读量,九(1)班对九年级800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A.10本以下;B.10~15本;C.16~20本;D.20本以上.根据统计整理并制作了如图所示的两幅统计图表:
(1)在这次调查中一共抽查了 名学生;
(2)表中x,y的值分别为:x= ,y= ;
(3)在扇形统计图中,C部分所对应的扇形的圆心角是 度;
(4)根据抽样调查结果,请估计九年级学生一年阅读课外书20本以上的学生人数.


查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南永州卷)数学(解析版) 题型:填空题
已知点A(1,y1),B(﹣2,y2)在反比例函数y=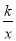 (k>0)的图象上,则y1 y2(填“>”“<”或“=”)
(k>0)的图象上,则y1 y2(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南株洲卷)数学(解析版) 题型:解答题
家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
(1)他下山时的速度比上山时的速度每小时快1千米;
(2)他上山2小时到达的位置,离山顶还有1千米;
(3)抄近路下山,下山路程比上山路程近2千米;
(4)下山用1个小时;
根据上面信息,他作出如下计划:
(1)在山顶游览1个小时;
(2)中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南常德卷)数学(解析版) 题型:选择题
如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于( )

A.30° B.45° C.60° D.75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com