
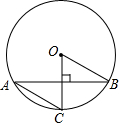
 如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )
如图,AB是⊙O的弦,半径OC⊥AB,AC∥OB,则∠BOC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
分析 由垂径定理、等腰三角形的性质和平行线的性质证出∠OAC=∠OCA=∠AOC,得出△OAC是等边三角形,得出∠BOC=∠AOC=60°即可.
解答 解:连接OA,
∵OC⊥AB,
∴$\widehat{AC}=\widehat{BC}$,
∴∠AOC=∠BOC,
∵OA=OC,AC∥OB,
∴∠OAC=∠OCA,BOC=∠OCA,
∴∠OAC=∠OCA=∠AOC,
∴△OAC是等边三角形,
∴∠BOC=∠AOC=60°;
故选:C.
点评 本题考查了垂径定理、等腰三角形的性质、平行线的性质、圆心角性质、等边三角形的判定与性质,熟练掌握垂径定理和等腰三角形的性质,证明△AOC是等边三角形是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
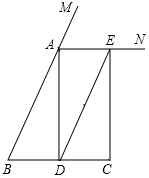 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
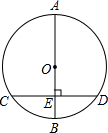 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )| A. | 10cm | B. | 14cm | C. | 15cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-y}{x+y}$=-$\frac{y-x}{y+x}$ | B. | $\frac{-a-b}{a+b}$=-1 | C. | $\sqrt{{(1-\sqrt{2})}^{2}}$=$\sqrt{2}$-1 | D. | $\sqrt{{a}^{2}}$=a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2000 | |
| B. | 湖州市2017年中考数学成绩 | |
| C. | 被抽取的2000名考生 | |
| D. | 被抽取的2000名考生的中考数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
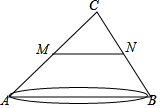 如图,有一池塘AB间的距离无法直接测量,小明在AB外取一点C,连接AC、BC,找到AC的中点M,BC的中点N,测得MN=40,则池塘AB间的距离( )
如图,有一池塘AB间的距离无法直接测量,小明在AB外取一点C,连接AC、BC,找到AC的中点M,BC的中点N,测得MN=40,则池塘AB间的距离( )| A. | 40 | B. | 20 | C. | 80 | D. | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com