
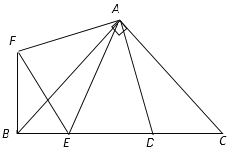
【题目】如图,在![]() 中,
中,![]()
![]() 是斜边
是斜边![]() 上两点,且
上两点,且![]() 将
将![]() 绕点
绕点![]() 顺时针旋转90°后,得到
顺时针旋转90°后,得到![]() 连接
连接![]()
(1)求证: △AED≌△AEF
(2)猜想线段BE,ED,DC之间的关系,并证明
【答案】(1)见解析 (2)![]() ,证明见解析
,证明见解析
【解析】
(1)由旋转的性质可得:AD=AF,∠BAC=∠FAD=90°,由![]() 可得∠FAE=
可得∠FAE=![]() ,所以
,所以![]() ,又AE=AE,故可证△AED≌△AEF
,又AE=AE,故可证△AED≌△AEF
(2)由旋转的性质可得:BF=CD,∠ACB=∠ABF,可证∠FBE=90°,由(1)可得:EF=ED,根据勾股定理可得:![]() ,故可得
,故可得![]()
∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,
∴AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,
∴∠DAE=∠FAE,
∵在△AED与△AEF中,
∴△AED≌△AEF(SAS)
(2)∵△AED≌△AEF,
∴ED=FE,∠ACB=∠ABF,
在Rt△ABC中,
∵∠ABC+∠ACB=90°,
∴∠ABC+∠ABF=90°即∠FBE=90°,
∴BE2+BF2=FE2,即BE2+DC2=DE2


科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,以每秒1单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是( )

A. 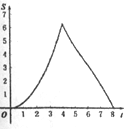 B.
B. 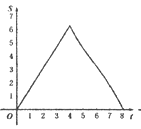
C. 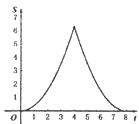 D.
D. 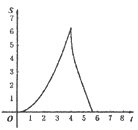
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在网上销售苹果,原计划每天卖100斤,但实际每天的销量与计划销量相比有出入,如表是某周7天的销售情况(超额记为正,不足记为负.单位:斤):

(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 斤;
(2)本周实际销售总量达到了计划销量没有?
(3)若每斤按5元出售,每斤苹果的运费为1元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C. 3 D. 5
C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
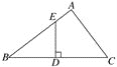
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 从
从![]() 点出发,先以每秒
点出发,先以每秒![]() 的速度运动到
的速度运动到![]() ,然后以每秒
,然后以每秒![]() 的速度从
的速度从![]() 运动到
运动到![]() .当点
.当点![]() 运动时间
运动时间![]() _______秒时,三角形
_______秒时,三角形![]() 的面积为
的面积为![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com