
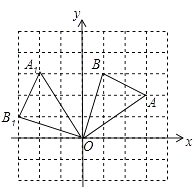
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A (3,2)、B(1,3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
(1)画出旋转后的图形;
(2)求线段OB在旋转过程中所扫过的图形面积(写过程)。
【答案】
(1)解:如图所示,则 ![]() 为所求作的图形;
为所求作的图形;
(2)解:点B扫过的图形为扇形 ![]() ,∵旋转角为90°,∴
,∵旋转角为90°,∴ ![]() =90°,∵点B(1,3),∴
=90°,∵点B(1,3),∴ ![]() ,∴
,∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据A 、B两点坐标,确定x轴和y轴,再将△AOB绕点O 逆时针旋转90°后得到△A1OB1,画出旋转后的图形。
(2)线段OB在旋转过程中所扫过的图形是以O为圆心,OB为半径的扇形,可知此扇形的圆心角为90°,再根据点B的坐标求出半径OB的长,即可求出此扇形的面积。
【考点精析】根据题目的已知条件,利用勾股定理的概念和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】已知AC平分∠PAQ,点B、B′分别在边AP、AQ上,如果添加一个条件,即可推出AB=AB′,下列条件中无法推出AB=AB′的是( )
A. BB′⊥AC B. BC=B′C C. ∠ACB=∠ACB′ D. ∠ABC=∠AB′C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点(-1,0),对称轴为:直线x=1,则下列结论中正确的是:( )
A.a>0
B.当x>1时,y随x的增大而增大
C.![]() <0
<0
D.x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《朗读者》节目的影响下,某中学开展了“好书伴我成长”读书活动.为了解5月份八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
关于这组数据,下列说法正确的是 ( )
A. 中位数是2 B. 众数是17 C. 平均数是3 D. 方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图像如图所示,则①abc;②b2-4ac;③2a+b;④a+b+c这四个式子中,值为负数的有个( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5, DC=3,求AC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,∠1+∠2=1800,∠3=∠4.
求证:EF∥GH.

证明:∵∠1+∠2=1800(已知),
∠AEG =∠1(对顶角相等)
∴ ,
∴AB∥CD( ),
∴∠AEG=∠ ( ),
∵∠3=∠4(已知),
∴∠3+∠AEG=∠4+∠ ,(等式性质)
∴ ,
∴EF∥GH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com