
【题目】如图,点O是直线AB上一点,∠AOD=120,∠AOC=90,OE平分∠BOD,则图中互为补角的角有__________对。

【答案】6
【解析】
根据图形,可得3对互补的角,再结合已知条件,利用角的和差以及角平分线的定义求出∠COD、∠DOE、∠BOE、∠COE的度数即可求得答案.
∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,∠AOD+∠BOD=180°,∠AOE+∠BOE=180°,
∵∠AOD=120°,∠AOC=90°,
∴∠BOD=180°-∠AOD=60°,∠COD=∠AOD-∠AOC=120°-90°=30°,
∵OE平分∠BOD,
∴∠BOE=∠DOE=30°,
∴∠COE=∠COD+∠DOE=60°,
∴∠AOD+∠COE=180°,
∠AOE+∠DOE=180°,∠AOE+∠COD=180°,
∴图中互补的角有6对,
故答案为:6.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A (3,2)、B(1,3)。△AOB绕点O 逆时针旋转90°后得到△A1OB1.
(1)画出旋转后的图形;
(2)求线段OB在旋转过程中所扫过的图形面积(写过程)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E,F 是ABCD 对角线上两点,在条件①DE=BF;②∠ADE=∠CBF; ③AF=CE;④∠AEB=∠CFD 中,添加一个条件,使四边形 DEBF 是平行四边形,可添加 的条件是( )
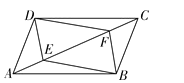
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1),B(﹣1,1),C(0,﹣2).
(1)写出点B关于坐标原点O对称的点B1的坐标;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.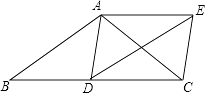
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知矩形ABCD的宽AD=8,点E在边AB上,P为线段DE上的一动点(点P与点D,E不重合),∠MPN=90°,M,N分别在直线AB,CD上,过点P作直线HK ![]() AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G
AB,作PF⊥AB,垂足为点F,过点N作NG⊥HK,垂足为点G
(1)求证:∠MPF=∠GPN
(2)在图1中,将直角∠MPN绕点P顺时针旋转,在这一过程中,试观察、猜想:当MF=NG时,△MPN是什么特殊三角形?在图2中用直尺画出图形,并证明你的猜想;
(3)在(2)的条件下,当∠EDC=30°时,设EP=x,△MPN的面积为S,求出S关于x的解析式,并说明S是否存在最小值?若存在,求出此时x的值和△MPN面积的最小值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如构造图1可以得到![]() .请解答下列问题:
.请解答下列问题:
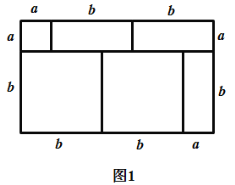
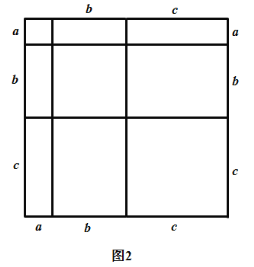
(1)仿照图1,构造适当的图形得到![]() 的值;
的值;
(2)写出图2中所表示的数学等式;
(3)利用(2)中所得到的结论,解决下面的问题:己知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com