
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中复习数学检测试卷(一)(解析版) 题型:单选题
下列变形中,从左向右是因式分解的是( )
A. x2﹣9+6x=(x+3)(x﹣3)+6x B. x2﹣8x+16=(x﹣4)2
C. (x﹣1)2=x2﹣2x+1 D. x2+1=x(x+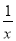 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.
定义:在平面直角坐标系xOy中,给定两点M(xM,yM),N(xN,yN),对于给定的实数a,b,作a|xM-xN|+b|yM-yN|为M,N的权重为a,b的直角距离,记为dxy(M,N),例如:d2,3((1,0),(4,7))=2|1-4|+3|0-7|=27.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18$\sqrt{2}$ | B. | 9$\sqrt{2}$ | C. | 18$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
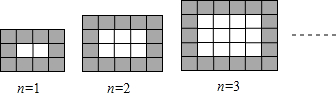
| A. | n2+6n+5 | B. | n2+5n+6 | C. | n2-6n+5 | D. | n2+5n-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com