
分析 (1)求出△的值,再进行判断即可;
(2)求出方程的两个根,再讨论即可.
解答 (1)证明:mx2-3(m+1)x+2m+3=0(m≠0),
∵△=[-3(m+1)]2-4m(2m+3)=m2+6m+9=(m+3)2,
∴当m≠0时,△≥0,
即该方程必有两个实数根;
(2)解:mx2-3(m+1)x+2m+3=0,
x=$\frac{3(m+1)±\sqrt{(m+3)^{2}}}{2m}$,
x1=2+$\frac{3}{m}$,x2=1,
要使$\frac{3}{m}$为整数,整数m可以为±1,±3,
∵该方程有两个不相等的整数根,
∴整数m的值是1,-1,3.
点评 本题考查了根的判别式和解一元二次方程的应用,能正确运用知识点进行计算是解此题的关键,用了分类讨论思想.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
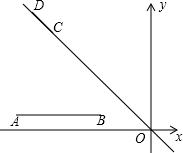 已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值.
已知线段AB,且A(-8,1)、B(-3,1),另有一线段CD在直线y=-x上,且CD=$\sqrt{2}$,确定D点位置,使A、B、C、D构成的四边形周长最短,并求D点坐标及这个最小值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
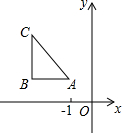 已知Rt△ABC位于第二象限,点A(-1,1),AB=BC=2,且两条直角边AB、BC分别平行于x轴、y轴,写出一个函数y=$\frac{k}{x}$(k≠0),使它的图象与△ABC有两个公共点,这个函数的表达式为y=-$\frac{5}{x}$.
已知Rt△ABC位于第二象限,点A(-1,1),AB=BC=2,且两条直角边AB、BC分别平行于x轴、y轴,写出一个函数y=$\frac{k}{x}$(k≠0),使它的图象与△ABC有两个公共点,这个函数的表达式为y=-$\frac{5}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
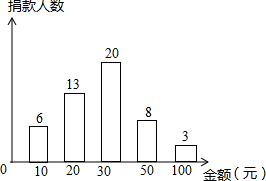 “只要人人都献出一点爱,世间将变成美好的人间”.在今年的慈善一日捐活动中,某中学九年级三班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图.根据如图提供的信息,捐款金额的众数和中位数分别是30,30.
“只要人人都献出一点爱,世间将变成美好的人间”.在今年的慈善一日捐活动中,某中学九年级三班50名学生自发组织献爱心捐款活动.班长将捐款情况进行了统计,并绘制成了统计图.根据如图提供的信息,捐款金额的众数和中位数分别是30,30.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)
已知:△ABC在直角坐标系中,A(-4,4),B(-4,0),C(-2,0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
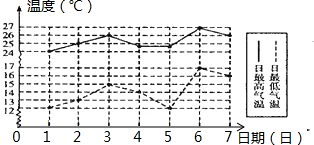 如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
如图是某城市6月份1日至7日每天的最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )| A. | 6月1日 | B. | 6月2日 | C. | 6月3日 | D. | 6月5日 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com