
【题目】某书商去图书批发市场购买某本书,第一次用12000元购书若干本,并把该书按定价7元/本出售,很快售完,由于该书畅销,书商又去批发市场采购该书,第二次购书时,每本书批发价已比第一次提高了20%,他用15000元所购书数量比第一次多了100本.
(1)求第一次购书的进价是多少元一本?第二次购进多少本书?
(2)若第二次购进书后,仍按原定价7元/本售出2000本时,出现滞销,书商便以定价的n折售完剩余的书,结果第二次共盈利100m元(n、m为正整数),求相应的n、m的值.
【答案】(1)第一次购书的进价为5元/本,且第二次买了2500本;(2)当n=4时,m=4;当n=6时,m=11;当n=8时,m=18.
【解析】
(1)设第一次购书的进价为x元/本,根据“第二次购书时,每本书批发价已比第一次提高了20%,他用15000元所购书数量比第一次多了100本”列出方程,求出方程的解即可得到结果;
(2)根据题意列出关于m与n的方程,由m与n为正整数,且n的范围确定出m与n的值即可.
(1)设第一次购书的进价为x元/本,
根据题意得:![]() ,
,
解得:x=5,
经检验x=5是分式方程的解,且符合题意,
∴15000÷(5×1.2)=2500(本),
则第一次购书的进价为5元/本,且第二次买了2500本;
(2)第二次购书的进价为5×1.2=6(元),
根据题意得:2000×(7-6)+(2500-2000)×(![]() -6)=100m,
-6)=100m,
整理得:7n=2m+20,即2m=7n-20,
∴m=![]() ,
,
∵m,n为正整数,且1≤n≤9,
∴当n=4时,m=4;当n=6时,m=11;当n=8时,m=18.


科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是∠BCA与∠ABC的平分线的交点,过O作与BC平行的直线分别交AB、AC于D、E.已知△ABC的周长为15,BC的长为6,求△ADE的周长.
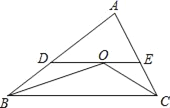
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为( ) 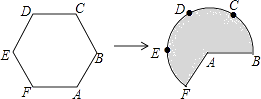
A.6π
B.18
C.18π
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
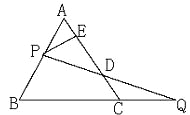
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,并在括号内注明理由.

(1)∵DE∥AB,( 已知 )
∴∠2= . ( , )
(2)∵DE∥AB,(已知 )
∴∠3= .( , )
(3)∵DE∥AB(已知 ),
∴∠1+ =180°.( , )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 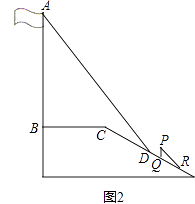
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com