Question

附加题：已知△ABC的三边长均为整数，△ABC的周长为奇数．
（1）若AC=8，BC=2，求AB的长；
（2）若AC-BC=5，求AB的最小值；
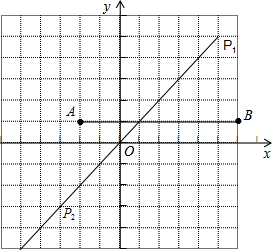
（3）若A（-2，1），B（6，1），在第一、三象限角平分线上是否存在点P，使△ABP的面积为16？若存在，求出P点坐标；若不存在，说明理由．

Answer 1

解：（1）由三角形的三边关系知，AC-BC＜AB＜AC+BC，
即：8-2＜AB＜8+2，∴6＜AB＜10，
又∵△ABC的周长为奇数，而AC、BC为偶数，
∴AB为奇数，故AB=7或9；

（2）∵AC-BC=5，
∴AC、BC中一个奇数、一个偶数，
又∵△ABC的周长为奇数，故AB为偶数，
AB＞AC-BC=5，得AB的最小值为6；

（3）存在．由A（-2，1），B（6，1）两点坐标可知：AB∥x轴，且AB=6-（-2）=8，
而△ABP的面积为16，由三角形计算面积公式可知，点P到AB的距离为4，
即P点纵坐标为5或-3，又P点在第一、三象限角平分线上，故P点坐标为（5，5）或（-3，-3）．
分析：（1）由三角形的三边关系知，AC-BC＜AB＜AC+BC，△ABC的周长为奇数，而AC、BC为偶数，故AB为奇数，在范围内求奇数AB的值；
（2）根据AC-BC=5可知：AC、BC中一个奇数、一个偶数，又△ABC的周长为奇数，故AB为偶数，再根据AC-BC＜AB＜AC+BC，求AB的最小值；
（3）存在．因为A（-2，1），B（6，1）两点在平行于x轴的直线上，且AB=6-（-2）=8，而△ABP的面积为16，由三角形计算面积公式可知，点P到AB的距离为4，又P点在第一、三象限角平分线上，由此可求P点坐标．
点评：本题考查了构成三角形边的条件的运用，数的奇偶性分析及坐标系中求三角形面积的问题．