
在-次数学活动课上,老师出了-道题:
(1)解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法)。
接着,老师请大家用自己熟悉的方法解第二道题:
(2)解关于x的方程mx2+(m一3)x一3=0(m为常数,且m≠0).
老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变式为第三道题:
(3)已知关于x的函数y=mx2+(m-3)x-3(m为常数).
①求证:不论m为何值,此函数的图象恒过x轴、y轴上的两个定点(设x轴上的定点为A,y轴上的定点为C);
②若m≠0时,设此函数的图象与x轴的另一个交点为反B,当△ABC为锐角三角形时,求m的取值范围;当△ABC为钝角三角形时,观察图象,直接写出m的取值范围.
请你也用自己熟悉的方法解上述三道题.

解:(1)由x2-2x-3=0,得(x+1)(x-3)=0∴x1=1,x2=3 …………3分
(2)方法一:由mx2+(m-3)x-3=0得(x+1)·(mx-3)=0
∵m≠0, ∴x1=-1,x2=![]() …………3分
…………3分
方法2:由公式法:![]()
∴x1=-1,x2=![]()
(3)①1°当m=0时,函数y= mx2+(m-3)x-3为y=-3x-3,令y=0,得x=-1
令x=0,则y=-3. ∴直线y=-3x-3过定点A(-1,0),C(0,-3) …………2分
2°当m≠0时,函数y= mx2+(m-3)x-3为y=(x+1)·(mx-3)
∴抛物线y=(x+1)·(mx-3)恒过两定点A(-1,0),C(0,-3)和B(![]() ,0)
,0)
②当m>0时,由①可知抛物线开口向上,且过点A(-1,0),C(0,-3)和
B(![]() ,0), …………1分
,0), …………1分
观察图象,可知,当⊿ABC为Rt⊿时,
则⊿AOC∽⊿COB∴![]()
∴![]() ∴32=1×
∴32=1×![]()
∴OB=9.即B(9,0)
∴当![]() .即:m>
.即:m>![]()
当m>![]() 时,⊿ABC为锐角三角形 …………2分
时,⊿ABC为锐角三角形 …………2分
 |

②观察图象可知
当0<m<![]() 时,则B点在(9,0)的右边时,∠ACB>90º,
时,则B点在(9,0)的右边时,∠ACB>90º,
当m<0且m≠-3时,点B在x轴的负半轴上,B与A不重合.
∴⊿ABC中的∠ABC>90º
∴⊿ABC是钝角三角形.
∴当0<m<![]() 或m<0且m≠-3时,
或m<0且m≠-3时,
⊿ABC为钝角三角形 …………2分


科目:初中数学 来源: 题型:
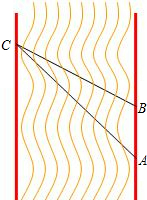 在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
在一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈| 3 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.
在一次数学活动课上,老师带领学生去测长江的宽度,某学生在长江北岸点A处观测到长江对岸水边有一点C,测得C在A东南方向上,沿长江边向东前行200米到达B处,测得C在B南偏东30°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:
 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com