
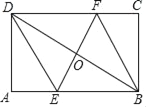
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)求证:△ADE≌△CBF;
(3)当四边形BEDF是菱形时,直接写出线段EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)EF=![]() .
.
【解析】
(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;(2)根据△BOE≌△DOF可知DE=BF,由AD=BC,∠DAE=∠BCF=90°即可证明△ADE≌△CBF;(3)设BE=x,在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE和△DOF中, ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)∵四边形BEDF是平行四边形,
∴DE=BF,
∵矩形ABCD,
∴∠DAE=∠BCF=90°,AD=BC,
在Rt△ADE与Rt△CBF中
![]() ,
,
∴Rt△ADE≌Rt△CBF(HL);
(3)当四边形BEDF是菱形时,BD⊥EF,
设BE=x,则 DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=![]() ,
,
∵BD=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∵BD⊥EF,
∴EO=![]() ,
,
∴EF=2EO=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.

(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:CN+CM=AC;
②如图2,当点M运动到线段BC之外(即点M在线段BC的延长线上时),其它条件不变(△ABC仍为等边三角形),请写出此时线段CN、CM、AC满足的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=![]() (x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).
(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的等边![]() 中,点D、E分别是边AC和AB的一点;
中,点D、E分别是边AC和AB的一点;
![]() 如图1,当
如图1,当![]() 时,连接BD、CE,设BD与CE交于点O,
时,连接BD、CE,设BD与CE交于点O,![]() 求证:
求证:![]() ;
;![]() 求
求![]() 的度数;
的度数;
![]() 如图2,点F是边BC的中点,点D是边AC的中点,过F作
如图2,点F是边BC的中点,点D是边AC的中点,过F作![]() 交边AB于点E,连接DE,请你利用目前所学知识试说明:
交边AB于点E,连接DE,请你利用目前所学知识试说明:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业加工一台大型机械设备润滑用油![]() 千克,用油的重复利用率为
千克,用油的重复利用率为![]() ,按此计算,加工一台大型机械设备的实际耗油量为
,按此计算,加工一台大型机械设备的实际耗油量为![]() 千克.通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现润滑用油量每减少
千克.通过技术革新后,不仅降低了润滑用油量,同时也提高了用油的重复利用率,并且发现润滑用油量每减少![]() 千克,用油量的重复利用率增加
千克,用油量的重复利用率增加![]() ,这样加工一台大型机械设备的实际耗油量下降到
,这样加工一台大型机械设备的实际耗油量下降到![]() 千克,问技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
千克,问技术革新后,加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点K,则∠BKI的大小为( )

A.90°B.84°C.72°D.88°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com