
【题目】把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点K,则∠BKI的大小为( )

A.90°B.84°C.72°D.88°
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过点D作AC的平行线交AB于点O,DE⊥AD交AB于点E.
(1)求证:点O是AE的中点;
(2)若点F是AC边上一点,且OF=OA,连接EF,如图2,判断EF与AC的位置关系,并说明理由;
(3)在(2)的条件下,试探究线段AE、AF、AC之间满足的等量关系,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
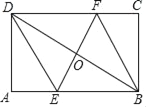
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB、CD边于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)求证:△ADE≌△CBF;
(3)当四边形BEDF是菱形时,直接写出线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()

![]() 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标;
![]() 求抛物线与
求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
![]() 画出抛物线的示意图;
画出抛物线的示意图;
![]() 根据图象回答:当
根据图象回答:当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而减小?
的增大而减小?
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲村和乙村靠近公路a、b,为了发展经济,甲乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:

(1)到两村的距离相等;
(2)到两条公路的距离相等.你能帮忙确定工厂的位置吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,证明:AB=FA+BD;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请画出图形并直接写出正确结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com