Question

【题目】如图1，在Rt△ABC中，∠ACB=90°，AD平分∠BAC，过点D作AC的平行线交AB于点O，DE⊥AD交AB于点E.

(1)求证：点O是AE的中点；

(2)若点F是AC边上一点，且OF=OA，连接EF，如图2，判断EF与AC的位置关系，并说明理由；

(3)在（2）的条件下，试探究线段AE、AF、AC之间满足的等量关系，并说明理由

Answer 1

【答案】（1）见解析；（2）EF⊥AC，理由见解析；（3）AE+AF=2AC，理由见解析．

【解析】

（1）根据直角三角形、角平分线和平行线的性质证明∠ODA=∠OAD，∠OED=∠ODE，进而得出OD=OA，OD=OE即可解决问题；
（2）结论：EF⊥AC．先证明OF=OE=OA，再根据等腰三角形的性质以及三角形内角和是180°即可解决问题；
（3）结论：AE+AF=2AC．延长ED交AC的延长线于M．证明AE=AM，CM=CF即可解决问题．

证明：如图1中，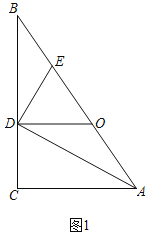

∵AD平分∠BAC，
∴∠CAD=∠BAD，
∵OD∥AC，
∴∠ODA=∠DAC，
∴∠ODA=∠OAD，
∴OD=OA，
∵DE⊥AD，
∴∠ADE=90°，
∴∠EDO+∠ADO=90°，∠DEO+∠OAD=90°，
∴∠OED=∠ODE，
∴OD=OE，
∴OE=OA，
∴点O是AE的中点；
（2）解：结论：EF⊥AC．
理由：如图2中，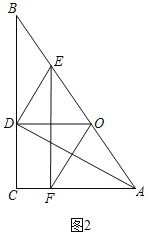

∵OF=OA，OA=OE，

∴OF=OE，∠OFA=∠OAF，

∴∠OEF=∠OFE，

∵∠OEF+∠OFE+∠OFA+∠OAF=180°，

∴∠OFE+∠OFA=90°，即∠EFA=90°，
∴EF⊥AC；
（3）解：如图3中，结论：AE+AF=2AC．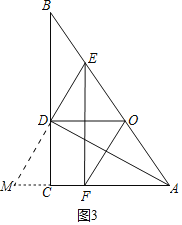

理由：延长ED交AC的延长线于M．
∵AD⊥EM，
∴∠ADM=∠ADE=90°，
∴∠M+∠DAM=90°，∠AED+∠DAE=90°，
∵∠DAM=∠DAE，
∴∠M=∠AED，
∴AE=AM，
∴DM=DE，
∵∠DCA=∠EFA=90°，
∴DC∥EF，
∵DM=DE，
∴CM=CF，
∵AE-AF=AM-AF=FM=2CF，AC-AF=CF，
∴AE-AF=2（AC-AF），
∴AE+AF=2AC．