
【题目】对于一元二次方程![]() ,下列说法:
,下列说法:
①若![]() ,方程
,方程![]() 有两个不等的实数根;
有两个不等的实数根;
②若方程![]() 有两个不等的实数根,则方程
有两个不等的实数根,则方程![]() 也一定有两个不等的实数根;
也一定有两个不等的实数根;
③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;
成立;
④若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立,其中正确的只有( )
成立,其中正确的只有( )
A. ①②④ B. ②③ C. ③④ D. ①④
【答案】D
【解析】
由a+c=0,a≠0,可知a、c异号,即可得△=b2-4ac>0,所以方程有两个不等的实数根,①正确;当c=0时不成立,②不正确;若c是方程ax2+bx+c=0的一个根,当c=0时,ac+b+1=0不一定成立,③不正确;若m是方程ax2+bx+c=0的一个根,所以有am2+bm+c=0,即am2= -(bm+c),而(2am+b)2=4a2m2+4abm+b2=4a[-(bm+c)]+4abm+b2=4abm-4abm-4ac+b2=b2-4ac,④正确.
①因为a+c=0,a≠0,所以①a、c异号,所以△=b2-4ac>0,所以方程有两个不等的实数根;
②当c=0时不成立;
③若c是方程ax2+bx+c=0的一个根,当c=0时,ac+b+1=0不一定成立;
④若m是方程ax2+bx+c=0的一个根,所以有am2+bm+c=0,即am2= -(bm+c),而(2am+b)2=4a2m2+4abm+b2=4a[-(bm+c)]+4abm+b2=4abm-4abm-4ac+b2=b2-4ac.
所以①④成立.
故选D.


科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
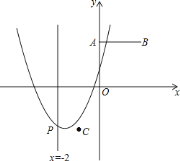
【题目】如图,已知点![]() ,
,![]() ,
,![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
![]() 当抛物线
当抛物线![]() 经过点
经过点![]() 时,求它的表达式;
时,求它的表达式;
![]() 设点
设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 的最小值,此时抛物线
的最小值,此时抛物线![]() 上有两点
上有两点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小;
的大小;
![]() 当抛物线
当抛物线![]() 与线段
与线段![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是![]() ”表示明天有
”表示明天有![]() 的时间降雨
的时间降雨
B. “抛一枚硬币正面朝上的概率是![]() ”表示每抛硬币
”表示每抛硬币![]() 次有
次有![]() 次出现正面朝上
次出现正面朝上
C. “彩票中奖的概率是![]() ”表示买
”表示买![]() 张彩票一定会中奖
张彩票一定会中奖
D. 不可能事件是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB垂线,交AC于E,交BC的延长线于F.

(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,过点D作AC的平行线交AB于点O,DE⊥AD交AB于点E.
(1)求证:点O是AE的中点;
(2)若点F是AC边上一点,且OF=OA,连接EF,如图2,判断EF与AC的位置关系,并说明理由;
(3)在(2)的条件下,试探究线段AE、AF、AC之间满足的等量关系,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com