Question

【题目】Rt△ABC中，∠B=90°∠A=30°．以C为圆心，小于BC长为半径画弧与AC、BC边交于点F、E．分别以E、F为圆心，大于EF为半径画弧，两弧交于点N，若BC= ， 则点M到AC的距离是（　　）

A.1
B.
C.
D.3

Answer 1

【答案】A
【解析】解：∵在Rt△ABC中，∠B=90°∠A=30°，
∴∠ACB=60°，
∵以C为圆心，小于BC长为半径画弧与AC、BC边交于点F、E．分别以E、F为圆心，大于EF为半径画弧，两弧交于点N，
∴∠ACM=∠MCB=30°，
∵∠B=90°，
∴CM=2BM，
∵BC= ，
∴由勾股定理得：BM2+（）2=（2BM）2 ，
解得：BM=1，
∵∠B=90°，∠ACM=∠BCM，
∴点M到AC的距离等于BM的长，即是1，
故选A．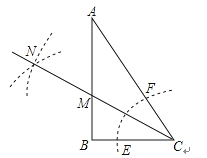

【考点精析】关于本题考查的角平分线的性质定理，需要了解定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能得出正确答案．