
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (0,6).
(0,6).
(1)求![]() ;
;
(2)求该抛物线的顶点坐标,并画出该抛物线的大致图像;
(3)试探索:在该抛物线上是否存在点P,使得以点P为圆心,以适当长为半径的⊙P与两坐标轴的正半轴都相切?如果存在,请求出点P的坐标和⊙P的半径;如果不存在,试说明理由.
【答案】(1)![]() ;
;
(2)抛物线的顶点(![]() ,
, ![]() ),大致图像见解析;
),大致图像见解析;
(3)抛物线上存在点P(![]() ,
,![]() ),使得以点P为圆心,以
),使得以点P为圆心,以![]() 为半径的圆与两坐标轴的正半轴都相切.
为半径的圆与两坐标轴的正半轴都相切.
【解析】试题分析:(1)将点C(0,6)代入抛物线y=-x2-x+c,得到关于c的方程,解方程可求c;(2)根据顶点坐标公式求顶点坐标,或把解析式配成顶点式确定顶点坐标,再画出该抛物线的大致图象;(3)设抛物线上存在点P(m,-m2-m+6),根据切线的性质可得m=-m2-m+6且m>0,解方程即可求解.
试题解析:(1)将![]() (0,6)代入
(0,6)代入![]() ,得
,得![]()
(2)把![]() 代入,得
代入,得![]()
∴
∴该抛物线的顶点(![]() ,
, ![]() )
)
大致图像如下

(3)设抛物线上存在点P(m, ![]() )
)

如图,要使⊙P与两坐标轴的正半轴都相切必需:
![]() 且
且![]()
解得![]() ,
, ![]() (舍去)
(舍去)
即抛物线上存在点P(![]() ,
,![]() ),使得以点P为圆心,
),使得以点P为圆心,
以![]() 为半径的圆与两坐标轴的正半轴都相切
为半径的圆与两坐标轴的正半轴都相切


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点A(﹣2,1)、B(﹣3,4)C(﹣5,2)均在格点上.在所给直角坐标系中解答下列问题:
将△ABC平移得△A1B1C1使得点B的对应点B1与原点O重合,在所给直角坐标系中画出图形;在图中画出△ABC关于y轴对称的△A2B2C2 , 并写出A2、B2、C2的坐标;在x轴上找一点P,使得△PAB2的周长最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于![]() EF为半径画弧,两弧交于点N,若BC=
EF为半径画弧,两弧交于点N,若BC=![]() , 则点M到AC的距离是( )
, 则点M到AC的距离是( )
A.1
B.![]()
C.![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
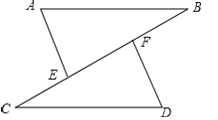
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需________根火柴( )

A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着电子技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占有面积0.00000065mm2 ,0.00000065用科学记数法表示为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com