
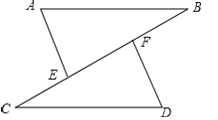
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (0,6).
(0,6).
(1)求![]() ;
;
(2)求该抛物线的顶点坐标,并画出该抛物线的大致图像;
(3)试探索:在该抛物线上是否存在点P,使得以点P为圆心,以适当长为半径的⊙P与两坐标轴的正半轴都相切?如果存在,请求出点P的坐标和⊙P的半径;如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知以下基本事实:①对顶角相等;②一条直线截两条平行线所得的同位角相等;③两条直线被第三条直线所截,若同位角相等,则这两条直线平行;④经过直线外一点,有且只有一条直线平行于已知直线.
(1)在利用以上基本事实作为依据来证明命题“两直线平行,内错角相等”时,必须要用的基本事实有____(填入序号即可);
(2)根据在(1)中的选择,结合所给图形,请你证明命题“两直线平行,内错角相等”,
已知:如图,_____________________________.
求证:________.
证明:____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:如图①,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=40°,求∠DEF的度数.
请将下面的解答过程补充完整,并填空(理由或数学式)
解:∵DE∥BC,∴∠DEF= .( )
∵EF∥AB,∴ =∠ABC.( )
∴∠DEF=∠ABC.(等量代换)
∵∠ABC=40°,∴∠DEF= °.
(2)应用:如图②,直线AB、BC、AC两两相交,交点分别为点A、B、C,点D在线段AB的延长线上,过点D作DE∥BC交AC于点E,过点E作EF∥AB交BC于点F.若∠ABC=60°,则∠DEF= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com