
【题目】在△ABC中,AB=AC,AB的中垂线于AC所在的直线相交所得的锐角为40°,则底角∠B的大小为
【答案】65°或25°
【解析】解:①DE与线段AC相交时,如图1,
∵DE是AB的垂直平分线,∠AED=40°,
∴∠A=90°﹣∠AED=90°﹣40°=50°,
∵AB=AC,
∴∠ABC=![]() (180°﹣∠A)=
(180°﹣∠A)=![]() (180°﹣50°)=65°;
(180°﹣50°)=65°;
②DE与CA的延长线相交时,如图2,∵DE是AB的垂直平分线,∠AED=40°,
∴∠EAD=90°﹣∠AED=90°﹣40°=50°,
∴∠BAC=180°﹣∠EAD=180°﹣50°=130°,
∵AB=AC,
∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣130°)=25°,
(180°﹣130°)=25°,
综上所述,等腰△ABC的底角∠B的大小为65°或25°.
故答案为:65°或25°.
作出图形,分①DE与线段AC相交时,根据直角三角形两锐角互余求出∠A,再根据等腰三角形两底角相等列式计算即可得解;②DE与CA的延长线相交时,根据直角三角形两锐角互余求出∠EAD,再求出∠BAC,然后根据等腰三角形两底角相等列式计算即可得解.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方.
如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作
(a≠0)记作![]() ,读作“a的圈n次方”.
,读作“a的圈n次方”.
(1)直接写出计算结果: ![]() _____,
_____, ![]() _________,
_________, ![]() ___________,
___________,
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,
请尝试将有理数的除方运算转化为乘方运算,归纳如下:一个非零有理数的圈 n 次方等于_____.
(3)计算 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.
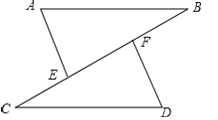
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需________根火柴( )

A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A,B,四边形ABCD是正方形,抛物线
轴分别相交于点A,B,四边形ABCD是正方形,抛物线![]() 在经过A,D两点.
在经过A,D两点.

(1)求该抛物线表达式;
(2)连接BD,将线段BD绕着D点顺时针旋转90度,得到DB’.直接写出点B’的坐标,并判断点B’是否落在抛物线上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果P点的坐标为(a,b),它关于y轴的对称点为P1,P1关于x轴的对称点为P2,已知P2的坐标为(-2,3),则点P的坐标为( )
A. (-2,-3) B. (2,-3) C. (-2,3) D. (2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com