Question

【题目】（1）探究：如图①，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=40°，求∠DEF的度数．

请将下面的解答过程补充完整，并填空（理由或数学式）

解：∵DE∥BC，∴∠DEF= ．（　　）

∵EF∥AB，∴ =∠ABC．（　　）

∴∠DEF=∠ABC．（等量代换）

∵∠ABC=40°，∴∠DEF= °．

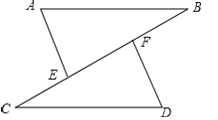
（2）应用：如图②，直线AB、BC、AC两两相交，交点分别为点A、B、C，点D在线段AB的延长线上，过点D作DE∥BC交AC于点E，过点E作EF∥AB交BC于点F．若∠ABC=60°，则∠DEF= °．

Answer 1

【答案】（1）答案见解析；（2）120．

【解析】试题分析：（1）依据两直线平行，内错角相等；两直线平行，同位角相，即可得到∠DEF=40°．

（2）依据两直线平行，内同位角相；两直线平行，同旁内角互补，即可得到∠DEF=180°-60°=120°．

试题解析：（1）∵DE∥BC，

∴∠DEF=∠EFC．（两直线平行，内错角相等）

∵EF∥AB，

∴∠EFC=∠ABC．（两直线平行，同位角相等）

∴∠DEF=∠ABC．（等量代换）

∵∠ABC=40°，

∴∠DEF=40°．

故答案为：∠EFC，两直线平行，内错角相等，∠EFC，两直线平行，同位角相等，40；

（2）∵DE∥BC，

∴∠ABC=∠EADE=60°．（两直线平行，内同位角相等）

∵EF∥AB，

∴∠ADE+∠DEF=180°．（两直线平行，同旁内角互补）

∴∠DEF=180°-60°=120°．

故答案为：120．