
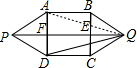
 如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是
如图,ABCD是一个正方形,P、Q是正方形外两点,且△APD和△BCQ是等边三角形,则∠PQD的正切值是



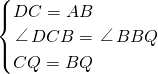 ,
, AD,
AD, BC.
BC. a,EF=a,在Rt△QEC中,由勾股定理,得
a,EF=a,在Rt△QEC中,由勾股定理,得 a,
a, a,
a,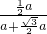 =2-
=2- .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
 如图1正方形ABCD是一个8行8列网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.
如图1正方形ABCD是一个8行8列网格电子屏的示意图,其中每个小正方形的边长为1.位于AD中点处的光点P按图2的程序移动.查看答案和解析>>
科目:初中数学 来源:2013-2014学年福建省九年级上学期期末质量抽测数学试卷(解析版) 题型:解答题
如图1,正方形ABCD是一个6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD中点处的点P按图2的程序动.
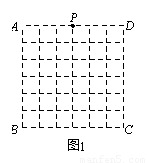
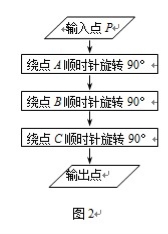
(1)请在图中画出点P经过的路径;
(2)求点P经过的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
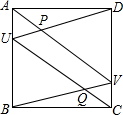 如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.
如图,ABCD是一个边长为1的正方形,U、V分别是AB、CD上的点,AV与DU相交于点P,BV与CU相交于点Q.求四边形PUQV面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com