若方程组$\left\{\begin{array}{l}{4x+3y=1}\\{kx+(k-1)y=3}\end{array}\right.$的解中x与y的值相等.则k的值是11．题目和参考答案——青夏教育精英家教网—

13．若方程组$\left\{\begin{array}{l}{4x+3y=1}\\{kx+（k-1）y=3}\end{array}\right.$的解中x与y的值相等，则k的值是11．

分析根据方程组$\left\{\begin{array}{l}{4x+3y=1}\\{kx+（k-1）y=3}\end{array}\right.$的解中x与y的值相等，可以求得k的值，从而可以解答本题．

解答解：∵方程组$\left\{\begin{array}{l}{4x+3y=1}\\{kx+（k-1）y=3}\end{array}\right.$的解中x与y的值相等，
∴$\left\{\begin{array}{l}{4x+3x=1}\\{kx+（k-1）x=3}\end{array}\right.$，
解得，$\left\{\begin{array}{l}{x=\frac{1}{7}}\\{k=11}\end{array}\right.$，
即k的值是11，
故答案为：11．

点评本题考查二元一次方程组的解，解答本题的关键是明确二元一次方程组的解得意义．

练习册系列答案

特级教师小学毕业升学系统总复习系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

3．

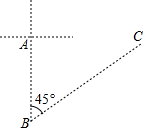距沿海某城市A的正南方向300km的B处有一台风中心，根据海事预报，以台风中心为圆心，200km为半径的圆形区域内会受到台风影响．该台风中心现在正以18km\h的速度沿北偏东45°方向往C移动，问：该城市是否会受到这次台风的影响？请说明理由．（$\sqrt{2}$≈1.4）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

4．

如图，计划把水从河中引到水池A中，先过点A作AB⊥CD，垂足为点B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是垂线段最短．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

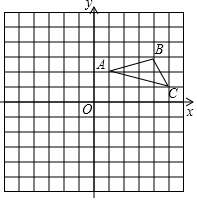在平面直角坐标系中，△ABC是格点三角形（三角形顶点在小方格顶点上），网格中小正方形的边长为1，请解答下列问题：
（1）将△ABC向下平移3个单位得到△A₁B₁C₁，作出平移后的△A₁B₁C₁．
（2）将△A₁B₁C₁经过适当方式进行图形变换后得到△A₂B₂C₂，使得△A₂B₂C₂与△ABC关于原点O成中心对称，请画出△A₂B₂C₂，并说出你是如何将△A₁B₁C₁进行图形变换后得到△A₂B₂C₂的．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

8．若x+y=5，则式子x²+2xy+y²+3的值为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．已知，梯形ABCD中，AB∥CD，BC⊥AB，AB=AD，连接BD（如图a），点P沿梯形的边，从点A→B→C→D→A移动，设点P移动的距离为x，BP=y．
（1）求证：∠A=2∠CBD；
（2）当点P从点A移动到点C时，y与x的函数关系如图（b）中的折线MNQ所示，试求CD的长．
（3）在（2）的情况下，点P从A→B→C→D→A移动的过程中，△BDP是否可能为等腰三角形？若能，请求出所有能使△BDP为等腰三角形的x的取值；若不能，请说明理由．