
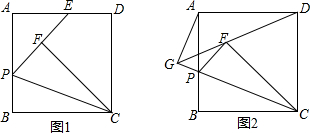
分析 (1)通过全等三角形Rt△CFE≌Rt△CDE(HL)的性质证得结论;
(2)如图2,过点A作AM⊥DG于点M,过点C作CN⊥DG于点N,构建全等三角形△AMD≌△DNC(AAS),由该全等三角形的性质和已知条件推知△CNG是等腰直角三角形,根据该等腰直角三角形的性质判定△AGM是等腰直角三角形,则AG=$\sqrt{2}$AM=$\frac{\sqrt{2}}{2}$DF,故$\frac{DF}{AG}$=$\sqrt{2}$;
(3)在直角△BCP中,由勾股定理得到PC=$\sqrt{P{B}^{2}+B{C}^{2}}$=$\frac{10}{3}$.然后结合相似三角形Rt△GAP∽Rt△BCP的对应边成比例得到:$\frac{PA}{PC}$=$\frac{GP}{BP}$,即GP=$\frac{2}{3}$.在直角△AGP中,AG=$\sqrt{A{P}^{2}-G{P}^{2}}$=2.由对角互补四边形模型可知:AG+GC=$\sqrt{2}$DG,由此求得DG的长度.
解答 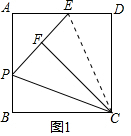 (1)证明:如图1,连接CE,
(1)证明:如图1,连接CE,
∵∠CFE=∠CDE=90°,BC=CF=CD,
∴Rt△CFE≌Rt△CDE(HL),
∴EF=DE;
(2)解:如图2,过点A作AM⊥DG于点M,过点C作CN⊥DG于点N
∴△AMD≌△DNC(AAS),
∴AM=DN,DM=CN.
∵CF=CD,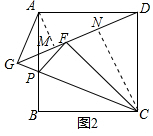
∴∠FCN=∠DCN.
又∵∠BCP=∠FCP,
∴∠NCP=45°,
∴△CNG是等腰直角三角形,
∴GN=CN=DM,
∴∠GM=DN=AM,
∴△AGM是等腰直角三角形,
∴AG=$\sqrt{2}$AM=$\frac{\sqrt{2}}{2}$DF,
∴$\frac{DF}{AG}$=$\sqrt{2}$;
(3)∵AB=$\sqrt{10}$,$\frac{BP}{AB}$=$\frac{1}{3}$,
∴BP=$\frac{\sqrt{10}}{3}$,AP=$\frac{2\sqrt{10}}{3}$.
在直角△BCP中,PC=$\sqrt{P{B}^{2}+B{C}^{2}}$=$\frac{10}{3}$.
∵Rt△GAP∽Rt△BCP,
∴$\frac{PA}{PC}$=$\frac{GP}{BP}$,即$\frac{\frac{2\sqrt{10}}{3}}{\frac{10}{3}}$=$\frac{GP}{\frac{\sqrt{10}}{3}}$,GP=$\frac{2}{3}$.
在直角△AGP中,AG=$\sqrt{A{P}^{2}-G{P}^{2}}$=2.
由对角互补四边形模型可知:AG+GC=$\sqrt{2}$DG,
∴DG=3$\sqrt{2}$.
故答案是:3$\sqrt{2}$.
点评 本题考查了相似综合题,需要掌握全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,等腰直角三角形的判定与性质,综合性比较强,难度一般.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
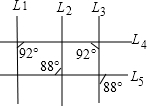 如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )
如图为平面上五条直线L1,L2,L3,L4,L5相交的情形,根据图中标示的角度,判断下列叙述何者正确( )| A. | L1和L3平行,L2和L3平行 | B. | L1和L3平行,L2和L3不平行 | ||
| C. | L1和L3不平行,L2和L3平行 | D. | L1和L3不平行,L2和L3不平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
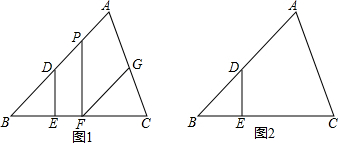
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
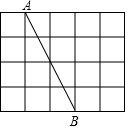 如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.
如图,在每个小正方形的边长为1的网格中,点A,B均在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com