练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    A、B两地相距48km，一艘轮船从A地顺流航行至B地，比从B地逆流航行至A地少用2h，已知水流速度为5km/h，求该轮船在静水中的航行速度是多少km/h？若设该轮船在静水中的速度为xkm/h，则可列方程（　　）

    A. =2 B. =2

    C. =2 D. =2

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年贵州省贵阳市七年级（上）期末数学试卷 题型：填空题

    国家规定初中每班的标准人数为a人，某中学七年级共有六个班，各班人数情况如下表

    班级

    七（1）班

    七（2）班

    七（3）班

    七（4）班

    七（5）班

    七（6）班

    与每班标准人数的差值

    +5

    +3

    ﹣5

    +4

    0

    ﹣2

    用含a的代数式表示该中学七年级学生总人数为_____人．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年湖北省襄阳市宜城市九年级（上）期末数学试卷 题型：解答题

    已知关于x的一元二次方程x2﹣4x+3m﹣2=0有两个不相等的实数根．

    （1）求m的取值范围；

    （2）当m为正整数时，求方程的根．

    查看答案和解析>>

    科目：初中数学 来源：湖北省恩施州利川市2017-2018学年八年级（上）期末数学试卷 题型：解答题

    如图①，在△ABC中，AB=AC，点P为边BC上异于B和C的任意一点，过点P作PD⊥AB于D，作PE⊥AC于E，过点C作CF⊥AB于F，求证：PD+PE=CF．

    （1）有下面两种证明思路：（一）如图②，连接AP，由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF．（二）如图②，过点P作PG⊥CF，垂足为G，可以证明：PD=GF，PE=CG，则PD+PE=CF．

    请你选择其中的一种证明思路完成证明：

    （2）探究：如图③，当点P在BC的延长线上时，其它条件不变，探究并证明PD、PE和CF间的数量关系；

    （3）猜想：当点P在CB的延长线上时，其它条件不变，猜想PD、PE和CF间的数量关系（不要求证明）

    查看答案和解析>>

    科目：初中数学 来源：湖北省恩施州利川市2017-2018学年八年级（上）期末数学试卷 题型：解答题

    计算（a﹣3b）（a+3b）﹣（﹣a﹣2b）（a﹣2b）

    查看答案和解析>>

    科目：初中数学 来源：湖北省恩施州利川市2017-2018学年八年级（上）期末数学试卷 题型：单选题

    若分式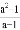有意义，则a满足的条件是（　　）

    A. a≠1的实数 B. a为任意实数 C. a≠1或﹣1的实数 D. a=﹣1

    查看答案和解析>>

    科目：初中数学 来源：山东省菏泽市鄄城县2017-2018学年八年级（上）期末数学试卷 题型：解答题

    某地出租车计费方法如图，x（km）表示行驶里程，y（元）表示车费，请根据图象解答下列问题：

    （1）该地出租车的起步价是 元；

    （2）当x＞2时，求y与x之间的函数关系式；

    （3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？

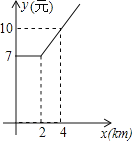
    查看答案和解析>>

    科目：初中数学 来源：山东省菏泽市鄄城县2017-2018学年八年级（上）期末数学试卷 题型：单选题

    如图，已知直线AB、CD被EF所截，GH交CD于D，∠EGB=∠BGH=∠ECD=50°，则∠CDH为（　　）

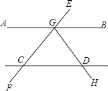
    A. 130° B. 150° C. 80° D. 100°

    查看答案和解析>>

    科目：初中数学 来源：湖北省鄂州市梁子湖区2017-2018学年七年级（上）期末数学试卷 题型：填空题

    已知点A在O的北偏西方向，点B在点O的南偏东方向，则的度数为______.

    查看答案和解析>>

    同步练习册答案