

科目:初中数学 来源:2008年全国中考数学试题汇编《圆》(12)(解析版) 题型:解答题
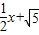 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.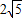 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.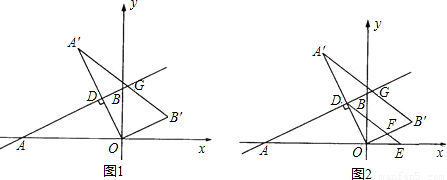
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《一次函数》(06)(解析版) 题型:解答题
 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.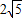 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.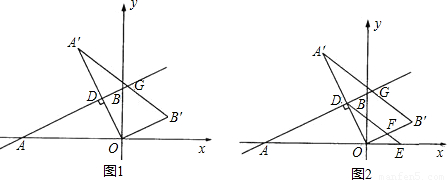
查看答案和解析>>
科目:初中数学 来源:2010年中考数学考前知识点回归+巩固 专题11 一次函数(解析版) 题型:解答题
 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒. 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2008年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题
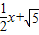 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.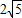 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.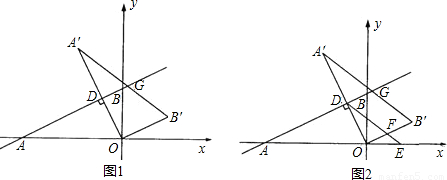
查看答案和解析>>
科目:初中数学 来源:2008年黑龙江省哈尔滨市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com