
【题目】已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x﹣2经过A、C两点,且AB=2.
(1)求抛物线的解析式;
(2)若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s= ![]() ,当t为何值时,s有最小值,并求出最小值.
,当t为何值时,s有最小值,并求出最小值.
(3)在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.
【答案】
(1)
解:由直线:y=x﹣2知:A(2,0)、C(0,﹣2);
∵AB=2,∴OB=OA+AB=4,即 B(4,0).
设抛物线的解析式为:y=a(x﹣2)(x﹣4),代入C(0,﹣2),得:
a(0﹣2)(0﹣4)=﹣2,解得 a=﹣ ![]()
∴抛物线的解析式:y=﹣ ![]() (x﹣2)(x﹣4)=﹣
(x﹣2)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)
解:在Rt△OBC中,OB=4,OC=2,则 tan∠OCB=2;
∵CE=t,∴DE=2t;
而 OP=OB﹣BP=4﹣2t;
∴s= ![]() =
= ![]() =
= ![]() (0<t<2),
(0<t<2),
∴当t=1时,s有最小值,且最小值为 1
(3)
解:在Rt△OBC中,OB=4,OC=2,则 BC=2 ![]() ;
;
在Rt△CED中,CE=t,ED=2t,则 CD= ![]() t;
t;
∴BD=BC﹣CD=2 ![]() ﹣
﹣ ![]() t;
t;
以P、B、D为顶点的三角形与△ABC相似,已知∠OBC=∠PBD,则有两种情况:
① ![]() =
= ![]()
![]() =
= ![]() ,解得 t=
,解得 t= ![]() ;
;
② ![]() =
= ![]()
![]() =
= ![]() ,解得 t=
,解得 t= ![]() ;
;
综上,当t= ![]() 或
或 ![]() 时,以P、B、D为顶点的三角形与△ABC相似
时,以P、B、D为顶点的三角形与△ABC相似
【解析】(1)首先根据直线AC的解析式确定点A、C的坐标,已知AB的长,进一步能得到点B的坐标;然后由待定系数法确定抛物线的解析式.(2)根据所给的s表达式,要解答该题就必须知道ED、OP的长;BP、CE长易知,那么由OP=OB﹣BP求得OP长,由∠CED的三角函数值可得到ED的长,再代入s的表达式中可得到关于s、t的函数关系式,结合函数的性质即可得到s的最小值.(3)首先求出BP、BD的长,若以P、B、D为顶点的三角形与△ABC相似,已知的条件是公共角∠OBC,那么必须满足的条件是夹公共角的两组对应边成比例,分两种情况讨论即可.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
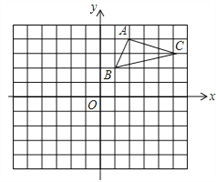
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标A1 ________________.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2__________________.
(3) △ABC是否为直角三角形?答_________(填是或者不是).
(4)利用格点图,画出BC边上的高AD,并求出AD的长,AD=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一天,龟、兔进行了600米赛跑,如图表示龟兔赛跑的路程s(米)与时间t(分钟)的关系(兔子睡觉前后速度保持不变),根据图象回答以下问题:
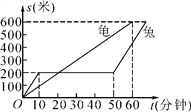
(1)赛跑中,兔子共睡了多少时间?
(2)赛跑开始后,乌龟在第几分钟时从睡觉的兔子旁经过?
(3)兔子跑到终点时,乌龟已经到了多长时间?并求兔子赛跑的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
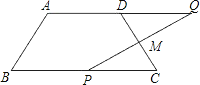
【题目】如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
(2)当点P在点B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)直接写出AB与AP所满足的数量关系:_____,AB与AP的位置关系:_____;
(2)将△ABC沿直线l向右平移到图2的位置时,EP交AC于点Q,连接AP,BQ,求证:AP=BQ;
(3)将△ABC沿直线l向右平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,试探究AP=BQ是否仍成立?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
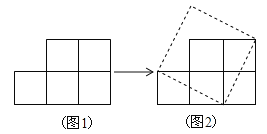
【题目】如图1.纸上有5个边长为1的小正方形组成的纸片,可把它剪拼成一个正方形(图2)
 (图3)
(图3)
拼成的正方体的面积与边长分别是多少?
你能把这十个小正方体组成的图形纸(图3),剪拼成一个大正方形吗?若能,则请画出剪拼成的大正方形,并求出其边长为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面题目的计算过程:
![]()
=![]() ①
①
=x﹣4﹣2(x﹣2)②
=x﹣4﹣2x+4③
=﹣x④
(1)上述计算过程中,从哪一步开始出现错误?请写出错误步骤的序号 ;
(2)错误原因是 ;
(3)写出本题的正确解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )

A. 2∠A=∠1﹣∠2 B. 3∠A=2(∠1﹣∠2)
C. 3∠A=2∠1﹣∠2 D. ∠A=∠1﹣∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com